【题目】如图所示,在四棱台![]() 中,
中, ![]() 底面
底面![]() ,四边形
,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() .
.
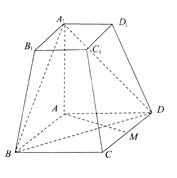
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】(Ⅰ)要证直线![]() 与平面
与平面![]() 垂直,现在由
垂直,现在由![]() 与底面垂直有
与底面垂直有![]() ,因此还要证一个垂直,证
,因此还要证一个垂直,证![]() ,这可通过等边三角形
,这可通过等边三角形![]() 得证
得证![]() ,从而有需要的结论
,从而有需要的结论![]() ,因此证得线面垂直;
,因此证得线面垂直;
(Ⅱ)要求直线与平面所成的角,分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
, ![]() 、
、![]() 、
、![]() 、
、 ,求出平面
,求出平面![]() 的法向量,由直线的方向向量与平面法向量夹角得线面角.
的法向量,由直线的方向向量与平面法向量夹角得线面角.
试题解析:(Ⅰ) ![]() 四边形为菱形,
四边形为菱形, ![]() ,连结
,连结![]() ,则
,则![]() 为等边三角形,
为等边三角形,
又![]() 为
为![]() 中点,
中点, ![]() ,由
,由![]() 得,
得, ![]() ,
,
![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,
, ![]() ,又
,又![]() ,
,
![]() 平面
平面![]()
(Ⅱ)![]() 四边形
四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
,
得![]() ,
, ![]() ,
, ![]() ,又
,又![]() 底面
底面![]() ,
,
分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]() ,
,
![]() 、
、![]() 、
、![]() 、
、 ,
,
 ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有 ,令
,令![]() ,则
,则![]()
![]() 直线
直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值
的正弦值
 .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
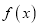 在
在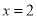 处取得极值,求实数
处取得极值,求实数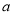 的值;
的值;(2)若函数
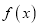 )在区间
)在区间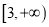 上为增函数,求实数
上为增函数,求实数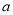 的取值范围;
的取值范围; (3)若当
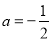 时,方程
时,方程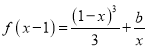 有实数根,求实数
有实数根,求实数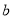 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市英才中学的一个社会实践调查小组,在对中学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对收回的120份有效问卷进行统计,得到如下
 列联表:
列联表:做不到光盘
能做到光盘
合计
男
45
10
55
女
30
15
45
合计
75
25
100
(1)现已按是否能做到光盘分层从45份女生问卷中抽取9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的份数为
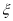 ,试求随机变量
,试求随机变量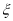 的分布列和数学期望;
的分布列和数学期望;(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过
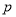 ,那么根据临界值表最精确的
,那么根据临界值表最精确的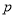 的值应为多少?请说明理由.
的值应为多少?请说明理由.附:独立性检验统计量
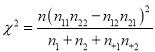 ,其中
,其中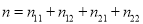 .
.独立性检验临界表:
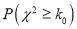
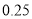

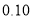
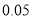
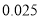
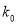
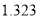
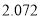
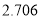
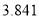
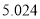
-
科目: 来源: 题型:
查看答案和解析>>【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三 年级一班至六班进行了“本届奥运会中国队表现”的满意度调查(结果只有“满意”和“不满意”两种),从被调查的学生中随机抽取了50人,具体的调查结果如下表:

(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为
 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
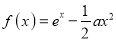 (
(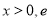 为自然对数的底数),
为自然对数的底数),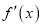 是
是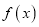 的导函数.
的导函数.(Ⅰ)当
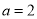 时,求证
时,求证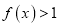 ;
;(Ⅱ)是否存在正整数
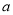 ,使得
,使得 对一切
对一切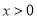 恒成立?若存在,求出
恒成立?若存在,求出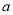 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】三个臭皮匠顶上一个诸葛亮,能顶得上吗?在一次有关“三国演义”的知识竞赛中,三个臭皮匠A、B、C能答对题目的概率分别为P(A)=
 ,P(B)=
,P(B)= ,P(C)=
,P(C)= ,诸葛亮D能答对题目的概率为P(D)=
,诸葛亮D能答对题目的概率为P(D)= ,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜?
,如果将三个臭皮匠A、B、C组成一组与诸葛亮D比赛,答对题目多者为胜方,问哪方胜? -
科目: 来源: 题型:
查看答案和解析>>【题目】海州市六一儿童节期间在妇女儿童活动中心举行小学生“海州杯”围棋比赛,规则如下:甲、乙两名选手比赛时,每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或赛满6局时比赛结束.设某校选手甲与另一选手乙比赛时,甲每局获胜的概率皆为
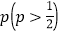 ,且各局比赛胜负互不影响,已知第二局比赛结束时比赛停止的概率为
,且各局比赛胜负互不影响,已知第二局比赛结束时比赛停止的概率为 .
.(1)求
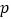 的值;
的值;(2)设
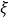 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量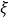 的分布列和数学期望
的分布列和数学期望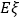 .
.
相关试题

