【题目】为提倡节能减排，同时减轻居民负担，广州市积极推进“一户一表”工程
非一户一表用户电费采用“合表电价”收费标准：
元
度“一户一表”用户电费采用阶梯电价收取，其11月到次年4月起执行非夏季标准如下：
第一档 | 第二档 | 第三档 | |
每户每月用电量 |
|
|
|
电价 |
|
|
|
例如：某用户11月用电410度，采用合表电价收费标准，应交电费
元，若采用阶梯电价收费标准，应交电费
元．
为调查阶梯电价是否能到“减轻居民负担”的效果，随机调查了该市100户的11月用电量，工作人员已经将90户的月用电量填在下面的频率分布表中，最后10户的月用电量
单位：度
为：88、268、370、140、440、420、520、320、230、380．
（1）在答题卡中完成频率分布表，并绘制频率分布直方图；
根据已有信息，试估计全市住户11月的平均用电量同一组数据用该区间的中点值作代表；
设某用户11月用电量为x度
，按照合表电价收费标准应交
元，按照阶梯电价收费标准应交
元，请用x表示和，并求当
时，x的最大值，同时根据频率分布直方图估计“阶梯电价”能否给不低于
的用户带来实惠？
【答案】（1）见解析（2）324度 （3）
的最大值为423，估计“阶梯电价”能给不低于
的用户带来实惠．
【解析】
（1）根据题意写出频率分布表，画出频率分布直方图即可；
（2）根据数据，同一组数据用该区间的中间值代表，计算11月的平均用电量即可；
(3)可得
，
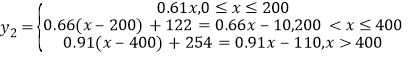，由题列不等式，计算可得x的取值范围及x的最大值，同时可得
时的频率，比较可得答案.
解：
频率分布表如下：
组别 | 月用电量 | 频数 | 频率 |
|
| 4 |
|
|
| 12 |
|
|
| 24 |
|
|
| 30 |
|
|
| 26 |
|
|
| 4 |
|
合计 | 100 | 1 |
频率分布直方图如下：
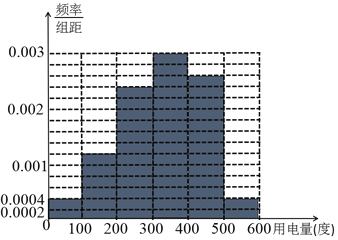
该100户用户11月的平均用电量：
度
所以估计全市住户11月的平均用电量为324度．
，
，
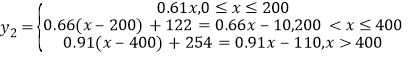由
，得
或
或
，
解得
，
，
的最大值为423．
根据频率分布直方图，时的频率为：
，
故估计“阶梯电价”能给不低于的用户带来实惠．
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案科目：高中数学 来源： 题型：
【题目】中国清朝数学家李善兰在1859年翻译《代数学》中首次将“
”译做：“函数”，沿用至今，为什么这么翻译，书中解释说“凡此变数中函彼变数者，则此为彼之函数”1930年美国人给出了我们课本中所学的集合论的函数定义，已知集合
，
，给出下列四个对应法则，请由函数定义判断，其中能构成从
到
的函数的是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公园要设计如图所示的景观窗格（其结构可以看成矩形在四个角处对称地截去四个全等的三角形所得，如图二中所示多边形
），整体设计方案要求:内部井字形的两根水平横轴
米，两根竖轴
米，记景观窗格的外框（如图二实线部分，轴和边框的粗细忽略不计）总长度为
米.
（1）若
，且两根横轴之间的距离为
米，求景观窗格的外框总长度；
（2）由于预算经费限制，景观窗格的外框总长度不超过
米，当景观窗格的面积（多边形的面积）最大时，给出此景观窗格的设计方案中
的大小与
的长度.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在空间直角坐标系
中，已知正四棱锥
的高
，点
和
分别在
轴和
轴上，且
，点
是棱
的中点.
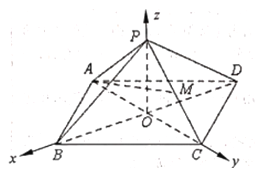
（1）求直线
与平面
所成角的正弦值；
（2）求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在直角坐标系xOy中，圆C的参数方程为
为参数
，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为
．
1求圆C的普通方程和直线l的直角坐标方程；
2设M是直线l上任意一点，过M做圆C切线，切点为A、B，求四边形AMBC面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)
男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:
，
，
，
，
，
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
其中
且
（i）当
时，若
，则实数
的取值范围是___________；
(ii) 若存在实数
使得方程
有两个实根，则实数
的取值范围是_______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，以
为极点，
轴正半轴为极轴建立极坐标系.已知曲线
的参数方程为
（
为参数），
，
为过点的两条直线，交于
，
两点，交于
，
两点，且的倾斜角为
，
.
（1）求和的极坐标方程；
（2）当
时，求点到，，，四点的距离之和的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
