（本题满分16分）
已知函数，且对任意，有.
（1）求；
（2）已知在区间（0，1）上为单调函数，求实数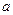的取值范围.
（3）讨论函数的零点个数？(提示：)


解：（1）由
得………………2分
（2）

所以………………4分
依题意，
或在（0，1）上恒成立………………6分
即
或在（0，1）上恒成立
由在（0，1）上恒成立，
可知
由在（0，1）上恒成立，
可知，所以或………………9分
（3），
令
所以………………10分
令，则，列表如下：

∴当时，函数无零点；
当1或时，函数有两个零点；
当时，函数有三个零点。
当时，函数有四个零点。………………16分

解析

关闭