【题目】已知点![]() ,圆
,圆![]() .
.
(1)若过点![]() 的圆的切线只有一条,求
的圆的切线只有一条,求![]() 的值及切线方程;
的值及切线方程;
(2)若过点![]() 且在两坐标轴上截距相等的直线与圆相切,求
且在两坐标轴上截距相等的直线与圆相切,求![]() 的值及切线方程.
的值及切线方程.
参考答案:
【答案】(1)![]() ,切线方程为
,切线方程为![]() 、
、![]() ;(2)切线方程为
;(2)切线方程为![]() 或
或![]() .
.
【解析】
试题分析:(1)过点![]() 的圆的切线只有一条,则
的圆的切线只有一条,则![]() 在圆上,将坐标代入圆,解得
在圆上,将坐标代入圆,解得![]() ,利用半径和切线垂直,求得切线的斜率,由此求得切线方程为
,利用半径和切线垂直,求得切线的斜率,由此求得切线方程为![]() 、
、![]() ;(2)依题意设直线方程截距式
;(2)依题意设直线方程截距式![]() ,将
,将![]() 的坐标代入,然后利用圆心到直线的距离等于半径,求得
的坐标代入,然后利用圆心到直线的距离等于半径,求得![]() 的值,进而求得切线方程.
的值,进而求得切线方程.
试题解析:
(1)由于过点![]() 的圆的切线只有一条,则点
的圆的切线只有一条,则点![]() 在圆上,故
在圆上,故![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,切线方程为
,切线方程为![]() ;
;
当![]() 时,
时,![]() ,切线方程为
,切线方程为![]() ,
,
∴![]() 时,切线方程为
时,切线方程为![]() ,
,
![]() 时,切线方程为
时,切线方程为![]() .
.
(2)设直线方程为![]() ,由于直线过点
,由于直线过点![]() ,∴
,∴![]() ,
,
∴直线方程为![]() ,即
,即![]() .
.
又直线与圆相切,∴![]() ,∴
,∴![]() ,
,
∴切线方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
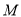 的圆心
的圆心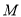 在
在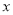 轴上,半径为1,直线
轴上,半径为1,直线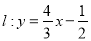 被圆
被圆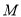 所截的弦长为
所截的弦长为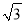 ,且圆心
,且圆心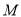 在直线
在直线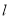 的下方.
的下方.(1)求圆
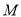 的方程;
的方程;(2)设
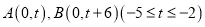 ,若圆
,若圆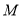 是
是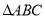 的内切圆,求
的内切圆,求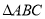 的面积
的面积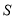 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
已知函数
 (
( 为常数)的图像与
为常数)的图像与 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为 .
.(1)求
 的值及函数
的值及函数 的极值;
的极值;(2)证明:当
 时,
时,
(3)证明:对任意给定的正数
 ,总存在
,总存在 ,使得当
,使得当 时,恒有
时,恒有
-
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:
 ,
, 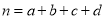 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①分类变量
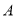 与
与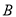 的随机变量
的随机变量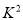 越大,说明“
越大,说明“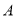 与
与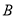 有关系”的可信度越大.
有关系”的可信度越大.②以模型
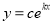 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设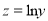 ,将其变换后得到线性方程
,将其变换后得到线性方程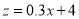 ,则
,则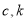 的值分别是
的值分别是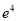 和0.3.
和0.3.③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为
 中,
中,  ,
,则
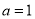 .正确的个数是( )
.正确的个数是( )A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
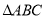 中, 角
中, 角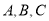 对边分别为
对边分别为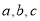 ,已知
,已知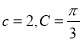 .
.(1)若
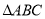 的面积等于
的面积等于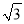 ,求
,求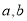 ;
;(2)若
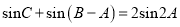 ,求
,求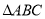 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
(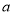 ﹥
﹥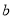 ﹥0)的离心率为
﹥0)的离心率为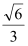 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为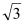 .
.(1)求椭圆
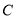 的方程;
的方程;(2)设直线
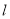 与椭圆
与椭圆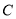 交于
交于 两点,坐标原点
两点,坐标原点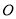 到直线
到直线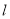 的距离为
的距离为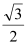 ,求
,求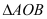 面积的最大值.
面积的最大值.
相关试题

