Question

 （本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分、第3小题满分6分．

设，常数，定义运算“”：，定义运算“”： ；对于两点、，定义.

(1)若，求动点的轨迹；

(2)已知直线与(1)中轨迹交于、两点，若，试求的值；

(3)在(2)中条件下，若直线不过原点且与轴交于点S，与轴交于点T，并且与(1)中轨迹交于不同两点P、Q , 试求的取值范围．

Answer 1

（1）（2）（3）（2，+）

解析:

(1)设,则

  （2分）     又由≥0可得

P(,)的轨迹方程为，轨迹C为顶点在原点，焦点为的抛物线在轴上及第一象限的内的部分                     （4分）

(2) 由已知可得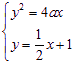  ,  整理得,

由 ,得．∵，∴   （6分）

∴

 ,           （8分）

解得或(舍) ；       （10分）

 (3)∵∴（12分）

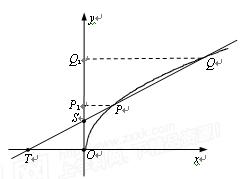
设直线,依题意,，则,分别过P、Q作PP??₁⊥y轴，QQ₁⊥y轴，垂足分别为P₁、Q₁，则．

由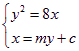消去y得

∴≥

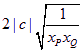
．   （14分）

∵、取不相等的正数，∴取等的条件不成立

 ∴的取值范围是（2，+）．                  （16分）