【题目】已知一三棱柱ABC﹣A1B1C1各棱长相等,B1在底面ABC上的射影是AC的中点,则异面直线AA1与BC所成角的余弦值为( )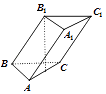
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:设AC的中点为O,连接BO、B1C,易知θ∠B1BC即为直线AA1与BC所成角.
并设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1,
则BO= ![]() ,在Rt△B1BO中,∵
,在Rt△B1BO中,∵ ![]() ,可得
,可得 ![]() .
.
在R△B1CO中,OC= ![]() ,可得
,可得 ![]()
在△BB1C中,由余弦定理,得cosθ= ![]() .
.
故选:B.
【考点精析】利用异面直线及其所成的角对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=x2﹣bx+alnx.
(1)若b=2,函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求实数a的取值范围;
(2)在(1)的条件下,证明:f(x2)>﹣ ;
;
(3)若对任意b∈[1,2],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点,焦点在
 轴上,离心率为
轴上,离心率为 的椭圆过点
的椭圆过点 .
.(1)求椭圆方程;
(2)设不过原点O的直线
 ,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为
,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为 ,满足
,满足 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输入的x的值为2,则输出的n的值为( )
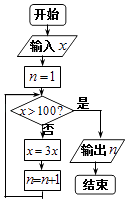
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E为AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量
 ,则λ+μ的最小值为 .
,则λ+μ的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了各个城市的大街小巷.为了解共享单车在
 市的使用情况,某调研机构在该市随机抽取了
市的使用情况,某调研机构在该市随机抽取了 位市民进行调查,得到的
位市民进行调查,得到的 列联表(单位:人)
列联表(单位:人)
(1)根据以上数据,能否在犯错误的概率不超过
 的前提下认为使用共享单车的情况与年龄有关?(结果保留3位小数)
的前提下认为使用共享单车的情况与年龄有关?(结果保留3位小数)(2)现从所抽取的
 岁以上的市民中利用分层抽样的方法再抽取5人
岁以上的市民中利用分层抽样的方法再抽取5人(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机抽取2人赠送一件礼物,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式及数据:
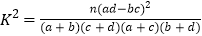 ,
, .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,且
,且  . (Ⅰ)试将y表示为x的函数f(x),并求f(x)的单调递增区间;
. (Ⅰ)试将y表示为x的函数f(x),并求f(x)的单调递增区间;
(Ⅱ)已知a、b、c分别为△ABC的三个内角A、B、C对应的边长,若 ,且
,且  ,a+b=6,求△ABC的面积.
,a+b=6,求△ABC的面积.
相关试题

