【题目】《九章算术》是我国古代数学经典名著，其中有这样一个问题：“今有圆材，埋在壁中，不知大小.以锯锯之，深一寸，锯道长一尺.问径几何？”其意为：今有－圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该木材，锯口深一寸，锯道长－尺.问这块圆柱形木材的直径是多少？现有长为1丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示（阴影部分为镶嵌在墙体内的部分）.已知弦尺，弓形高寸，估算该木材镶嵌在墙体中的体积约为__________立方寸.（结果保留整数）

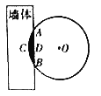
注：l丈＝10尺＝100寸，，.

【答案】633

【解析】

由题意画出图形，求出圆柱的底面半径，进一步求出弓形面积，代入体积公式得答案．

如图所示：

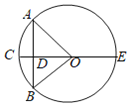
（寸，则（寸，（寸，

设圆的半径为（寸，则（寸，

在中，由勾股定理可得：，解得：（寸．

，即，则．

则弓形的面积（平方寸）．

则算该木材镶嵌在墙中的体积约为（立方寸）．

故答案为：633.

关闭