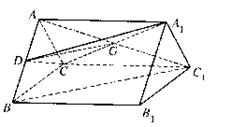
(本小题共12分)
如图,在正三棱柱ABC—A1B1C1中,点D是棱AB的中点,BC=1,AA1=
(1)求证:BC1//平面A1DC;
(2)求二面角D—A1C—A的大小

【答案】

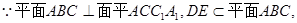
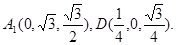
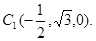 …6分 设平面A1DC的法向量为
…6分 设平面A1DC的法向量为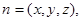
(1)略
(2)设二面角D—A1C—A的大小为
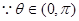
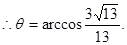
【解析】(I)证明:连结AC1交A1C于点G,连结DG,
在正三棱柱ABC—A1B1C1中,四边形ACC1A1是平行四边形,
|

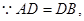
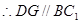 …………2分
…………2分

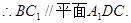 …………4分
…………4分
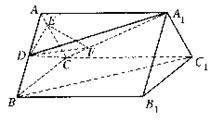
(II)解法一: 过点D作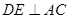 交AC于E,过点D作
交AC于E,过点D作 交A1C于F,连结EF。
交A1C于F,连结EF。
|
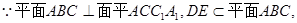
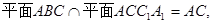
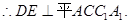

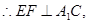
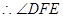 是二面角D—A1C—A的平面角,…………8分
是二面角D—A1C—A的平面角,…………8分
在直角三角形ADC中,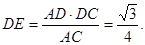
同理可求: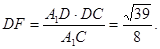

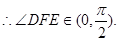
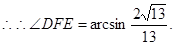 …………12分
…………12分
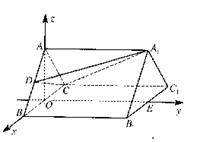
解法二:过点A作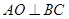 交BC于O,过点O作
交BC于O,过点O作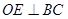 交B1C1于E。
交B1C1于E。
因为平面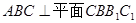
所以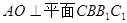 ,分别以CB、OE、OA所在的直线为
,分别以CB、OE、OA所在的直线为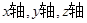 建立空间直角坐标系,
建立空间直角坐标系,
如图所示,因为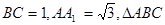 是等边三角形,所以O为BC的中点,则
是等边三角形,所以O为BC的中点,则 
|
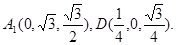
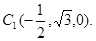 …6分 设平面A1DC的法向量为
…6分 设平面A1DC的法向量为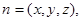
则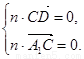
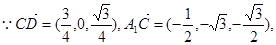
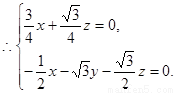
取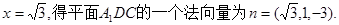 ……8分
……8分
可求平面ACA1的一个法向量为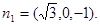 …………10分
…………10分
设二面角D—A1C—A的大小为
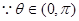
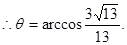 …………12分
…………12分