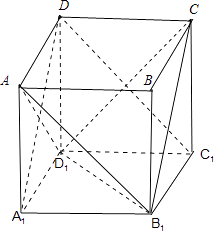
【题目】如图是从上下底面处在水平状态下的棱长为a的正方体ABCD﹣A1B1C1D1中分离出来的: 
(1)试判断A1是否在平面B1CD内;(回答是与否)
(2)求异面直线B1D1与C1D所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积的水.
参考答案:
【答案】
(1)解:是.补全正方体如图所示:
证明如下:连接A1D、B1C,∵A1B1∥DC,A1B1=DC,
∴四边形A1B1CD是平行四边形,
∴A1是在平面B1CD内
(2)解:连接AB1、AD1,∵对角面AB1C1D是矩形,∴AB1∥DC1,
∴∠AB1D1或其补角是异面直线B1D1与C1D所成的角.
∵AD1=AB1=D1B1,∴△AB1D1是正三角形.
∴∠AB1D1=60°.
∴异面直线B1D1与C1D所成的角是60°
(3)解:题目中的图形一个装置来盛水,那么盛最多体积的水时应是
三棱锥C1﹣B1CD1的体积.
又 ![]() .
.
∴用图示中这样一个装置来盛水,那么最多可以盛 ![]() 体积的水.
体积的水.
【解析】(1)利用正方体对角面是平行四边形的性质即可得出;(2)利用对角面的性质、表面对角线组成的△AB1D1是等边三角形即可求出;(3)题目中的图形一个装置来盛水,那么盛最多体积的水时应是三棱锥C1﹣B1CD1的体积.
【考点精析】掌握异面直线及其所成的角是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:y=x+m﹣2的图象不经过第二象限,命题q:方程x2+
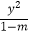 =1表示焦点在x轴上的椭圆. (Ⅰ)试判断p是q的什么条件;
=1表示焦点在x轴上的椭圆. (Ⅰ)试判断p是q的什么条件;
(Ⅱ)若p∧q为假命题,p∨q为真命题,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=3x
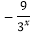 .
.(1)若f(x)=8,求x的值;
(2)对于任意的x∈[0,2],[f(x)-3]3x+13-m≥0恒成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数f(x)=sinx的图象向右平移
 个单位,横坐标缩小至原来的
个单位,横坐标缩小至原来的 倍(纵坐标不变)得到函数y=g(x)的图象.
倍(纵坐标不变)得到函数y=g(x)的图象.(1)求函数g(x)的解析式;
(2)若关于x的方程2g(x)-m=0在x∈[0,
 ]时有两个不同解,求m的取值范围.
]时有两个不同解,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是菱形,且
是菱形,且 .点
.点 是棱
是棱 的中点,平面
的中点,平面 与棱
与棱 交于点
交于点 .
.
(1)求证:
 ∥
∥ ;
;(2)若
 ,且平面
,且平面 平面
平面 ,求平面
,求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=log2(3-x).
(1)若g(x)=f(2+x)+f(2-x),判断g(x)的奇偶性;
(2)记h(x)是y=f(3-x)的反函数,设A、B、C是函数h(x)图象上三个不同的点,它们的纵坐标依次是m、m+2、m+4且m≥1;试求△ABC面积的取值范围,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
 ,
, ,则函数
,则函数 的图像经过怎样的变换可以得到函数
的图像经过怎样的变换可以得到函数 的图像
的图像 ①先向左平移
 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的 倍,纵坐标保持不变.
倍,纵坐标保持不变.②先向左平移
 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的 倍,纵坐标保持不变.
倍,纵坐标保持不变.③将横坐标缩短到原来的
 倍,再向左平移
倍,再向左平移 个单位,纵坐标保持不变.
个单位,纵坐标保持不变.④将横坐标缩短到原来的
 倍,再向左平移
倍,再向左平移 个单位,纵坐标保持不变.
个单位,纵坐标保持不变.A. ①③B. ①④C. ②③D. ②④
相关试题

