【题目】已知函数![]() 在x = 2处的切线与直线
在x = 2处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)若存在![]() ,使
,使![]() 成立,求m的最小值.
成立,求m的最小值.
参考答案:
【答案】(Ⅰ)函数f (x)的单调递减区间是(0,1],单调递增区间是[1,+∞);(Ⅱ)m的最小值是5.
【解析】试题分析:1)求出函数的导数,根据f′(2)的值,求出a,从而求出函数的单调区间;
(2)问题等价于当x∈(1,+∞)时,![]() 成立,设
成立,设![]() ,根据函数的单调性判断即可.
,根据函数的单调性判断即可.
试题解析:
(Ⅰ)![]()
由已知,![]() ,解得:a = 1
,解得:a = 1
∴![]()
当![]() 时,
时,![]() ,f (x)是减函数
,f (x)是减函数
当![]() 时,
时,![]() ,f (x)是增函数
,f (x)是增函数
∴函数f (x)的单调递减区间是(0,1],单调递增区间是[1,+∞).
(Ⅱ)解:∵![]() ,∴
,∴![]() 等价于
等价于![]()
即存在![]() ,使
,使![]() 成立,∴
成立,∴![]()
设![]() ,则
,则![]()
设![]() ,则
,则![]()
∴h (x)在![]() 上单调递增.
上单调递增.
又h (3) < 0,h (4) > 0,∴h (x)在![]() 上有唯一零点,设为x0,则
上有唯一零点,设为x0,则![]() ,且
,且![]()
![]()
又![]() ,∴m的最小值是5.
,∴m的最小值是5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,几何体是圆柱的一部分,它是由矩形
 (及其内部)以
(及其内部)以 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转 得到的,
得到的,  是
是 的中点.
的中点.(
 )设
)设 是
是 上的一点,且
上的一点,且 ,求
,求 的大小;
的大小;(
 )当
)当 时,求二面角
时,求二面角 的大小.
的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在
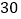 人或
人或 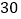 人以下,每人需交费用为
人以下,每人需交费用为 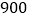 元;若旅行团人数多于
元;若旅行团人数多于 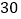 人,则给予优惠:每多
人,则给予优惠:每多 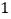 人,人均费用减少
人,人均费用减少 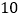 元,直到达到规定人数
元,直到达到规定人数 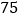 人为止.旅行社需支付各种费用共计
人为止.旅行社需支付各种费用共计 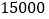 元.
元.Ⅰ 写出每人需交费用
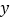 关于人数
关于人数 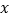 的函数;
的函数;Ⅱ 旅行团人数为多少时,旅行社可获得最大利润?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,
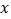 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线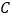 的极坐标方程为
的极坐标方程为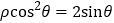 ,它在点
,它在点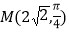 处的切线为直线
处的切线为直线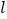 .
.(Ⅰ)求直线
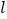 的直角坐标方程;
的直角坐标方程;(Ⅱ)已知点
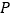 为椭圆
为椭圆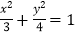 上一点,求点
上一点,求点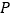 到直线
到直线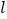 的距离的取值范围.
的距离的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
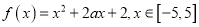
(1)若
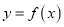 在
在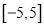 上是单调函数,求实数
上是单调函数,求实数 取值范围.
取值范围.(2)求
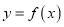 在区间
在区间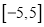 上的最小值.
上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道, 莫言是中国首位获得诺贝尔奖的文学家, 国人欢欣鼓舞.某高校文学社从男女生中各抽取
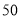 名同学调查对莫言作品的了解程度, 结果如下:
名同学调查对莫言作品的了解程度, 结果如下:阅读过莫言的作品数( 篇)

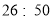

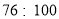
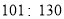
男生
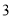
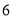
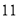

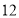
女生
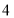
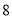
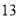
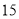
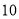
(1)试估计该校学生阅读莫言作品超过
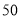 篇的概率;
篇的概率; (2)对莫言作品阅读超过
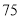 篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过
篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过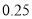 的前提下, 认为对莫言作品非常了解与性别有关?
的前提下, 认为对莫言作品非常了解与性别有关? 非常了解
一般了解
合计
男生
女生
合计
附:
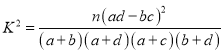 ,其中
,其中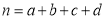
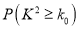
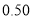

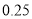
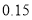
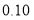

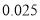
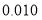
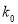
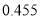
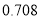

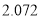

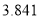
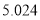

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
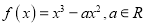 .
.(1)求
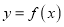 的单调区间;
的单调区间;(2)若曲线
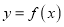 与直线
与直线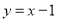 只有一个交点, 求实数
只有一个交点, 求实数 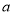 的取值范围.
的取值范围.
相关试题

