【题目】已知椭圆 的焦点坐标分別为,,为椭圆上一点，满足且

(1) 求椭圆的标准方程:

(2) 设直线与椭圆交于两点，点，若，求的取值范围.

【答案】（1）；（2）

【解析】分析：第一问首先根据题中条件将涉及到的量设出来，之后结合椭圆的定义以及对应的线段的倍数关系，求得对应的边长，利用余弦定理借用余弦值建立边之间的等量关系式，从而求得的值，借用椭圆中的关系，求得b的值，从而求得椭圆的方程，第二问将直线的方程与椭圆的方程联立，求得两根和与两根积，从而求得线段的中点，利用条件可得垂直关系，建立等量关系式，借用判别式大于零找到其所满足的不等关系，求得k的取值范围.

详解：（1）由题意设，则，又，，

在 中，由余弦定理得， ，

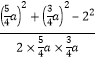
解得，，，所求椭圆方程为

（2）联立方程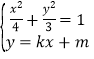，消去得 ，

则 ，，且…①

设的中心为，则 ，，

,,即， ，解得…②

把②代入①得，整理得，即

解得

关闭