【题目】已知函数f（x）＝x2+tx+1（其中实数t＞0）．

（1）已知实数x1，x2∈[﹣1，1]，且x1＜x2．若t＝3，试比较x1f（x1）+x2f（x2）与x1f（x2）+x2f（x1）的大小关系，并证明你的结论；

（2）记g（x），若存在非负实数x1，x2，…xn+1，使g（x1）+g（x2）+…+g（xn）＝g（xn+1）（n∈N*）成立，且n的最大值为8，求实数t的取值范围．

【答案】（1）x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1）；见解析（2）[22，25）．

【解析】

（1）利用作差比较法，结合函数f（x）的单调性进行求解即可；

（2）存在非负实数x1，x2，…xn+1，使g（x1）+g（x2）+…+g（xn）＝g（xn+1）（n∈N*）成立，且n的最大值为8，因此有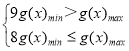成立，求出g（x）的表达式，利用基本不等式，分类讨论求出的最值，最后求出实数t的取值范围.

（1）x1f（x1）+x2f（x2）﹣x1f（x2）﹣x2f（x1）＝（x1﹣x2）（f（x1）﹣f（x2）），

∵t＝3，

∴f（x）＝x2+3x+1在[﹣1，1]上单调递增，

由x1，x2∈[﹣1，1]，且x1＜x2知，f（x1）＜f（x2），

∴（x1﹣x2）（f（x1）﹣f（x2））＞0，

∴x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1）；

（2）∵存在非负实数x1，x2，…xn+1，使g（x1）+g（x2）+…+g（xn）＝g（xn+1）（n∈N*）成立，且n的最大值为8，

∴，

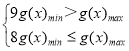下面求的最值，

当x＝0时，g（0）＝1；

当x＞0时，，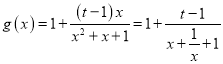

∵，

∴，

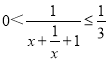①当t＝1时，g（x）＝1，不合题意；

②当0＜t＜1时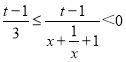，，故函数g（x）的值域为，

可得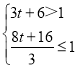，解得（不符，舍去）；

③当t＞1时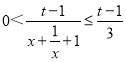，，故函数g（x）的值域为，

可得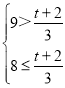，解得22≤t＜25；

综上所述，实数t的取值范围为[22，25）．

关闭