【题目】对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则把
,则把![]() 叫闭函数。
叫闭函数。
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)已知![]() 是正整数,且定义在
是正整数,且定义在![]() 的函数
的函数![]() 是闭函数,求正整数
是闭函数,求正整数![]() 的最小值,及此时实数k的取值范围。
的最小值,及此时实数k的取值范围。
参考答案:
【答案】(1)![]() ;(2)不是,理由见解析;(3)
;(2)不是,理由见解析;(3)![]() 。
。
【解析】
试题分析:(1)由题意,![]() 在
在![]() 上递减,在
上递减,在![]() 上的值域为
上的值域为![]() ,故有
,故有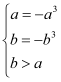 ,求得
,求得![]() 、
、![]() 的值,可得结论;(2)取
的值,可得结论;(2)取![]() ,则由
,则由![]() ,可得
,可得![]() 不是
不是![]() 上的减函数。同理求得
上的减函数。同理求得![]() 不是
不是![]() 上的增函数,从而该函数不是闭函数;(3)由题意,可得方程
上的增函数,从而该函数不是闭函数;(3)由题意,可得方程![]() 在
在![]() 上有两个不等的实根.利用基本不等式求得当
上有两个不等的实根.利用基本不等式求得当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .再根据函数
.再根据函数![]() 在
在![]() 上递减,在
上递减,在![]() 递增,而函数
递增,而函数![]() 与
与![]() 在
在![]() 有两个交点,可得正整数
有两个交点,可得正整数![]() 的最小值为
的最小值为![]() ,此时,
,此时,![]() ,由此求得
,由此求得![]() 的范围。
的范围。
试题解析:(1)由题意,![]() 在
在![]() 上递减,则
上递减,则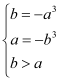 解得
解得![]() 所以,所求的区间为
所以,所求的区间为![]() 。
。
(2)取![]() 则
则![]() ,即
,即![]() 不是
不是![]() 上的减函数。取
上的减函数。取![]()
![]() ,即
,即![]() 不是
不是![]() 上的增函数。所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
上的增函数。所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)![]() 是闭函数,则存在区间
是闭函数,则存在区间![]() ,使函数
,使函数![]() 的值域为
的值域为![]() ,
,![]() 在
在![]() 单调递增,即
单调递增,即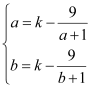 ,
,![]() 为方程
为方程![]() 的两个实根,即方程
的两个实根,即方程![]() 在
在![]() 上有两个不等的实根。
上有两个不等的实根。![]() ,当且仅当
,当且仅当![]() 时取等号考察函数
时取等号考察函数![]()
∵函数![]() 在
在![]() 上递减,∴
上递减,∴![]() 。
。
∵![]() 在
在![]() 递增,而函数
递增,而函数![]() 与
与![]() 在
在![]() 有两个交点。
有两个交点。
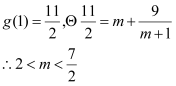
所以正整数![]() 的最小值为
的最小值为![]() ,
,![]() ,此时
,此时![]() 的取值范围为
的取值范围为![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】请设计一份问卷调查你们班同学阅读课外书的情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近视地表示为
 ,已知此生产线的年产量最大为210吨.
,已知此生产线的年产量最大为210吨.(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.

(Ⅰ)要使矩形AMPN的面积大于32平方米,则DN的长应在什么范围内?
(Ⅱ)当DN的长为多少时,矩形花坛AMPN的面积最小?并求出最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机
 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为 万元,且
万元,且
(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万只)的函数解析式;
(万只)的函数解析式;(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,已知椭圆
中,已知椭圆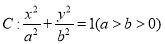 的离心率为
的离心率为 ,经过椭圆的左顶点
,经过椭圆的左顶点 作斜率为
作斜率为 的直线
的直线 交椭圆
交椭圆 于点
于点 ,交
,交 轴于点
轴于点 .
.
(1)求椭圆
 的方程;
的方程;(2)已知点
 为线段
为线段 的中点,
的中点, 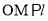 ,并且
,并且 交椭圆
交椭圆 于点
于点 .
.①是否存在定点
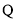 ,对于任意的
,对于任意的 都有
都有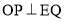 ?若存在,求出点
?若存在,求出点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;②求
 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点 都在函数
都在函数 的图象上,记
的图象上,记 与
与 的等差中项为
的等差中项为 。
。(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)若
 ,求数列
,求数列 的前
的前 项和
项和 ;
;(Ⅲ)设集合
 ,等差数列
,等差数列 的任意一项
的任意一项 ,其中
,其中 是
是 中的最小数,且
中的最小数,且 ,求
,求 的通项公式。
的通项公式。
相关试题

