【题目】命题:“若ab=0,则a=0或b=0”的逆否命题是 ______.
参考答案:
【答案】若a≠0且b≠0,则ab≠0
【解析】“若ab=0,则a=0或b=0”的逆否命题是:若a≠0且b≠0,则ab≠0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
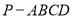 中,平面
中,平面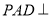 平面
平面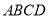 ,
,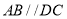 ,
,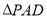 是等边三角形.已知
是等边三角形.已知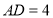 ,
,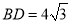 ,
,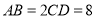 .
.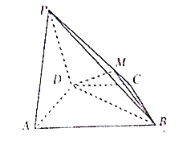
(1)设
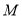 是
是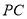 上的一点,证明:平面
上的一点,证明:平面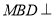 平面
平面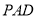 ;
;(2)当
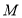 点位于线段
点位于线段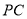 什么位置时,
什么位置时,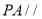 平面
平面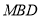 ?
?(3)求四棱锥
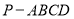 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合P={x| x2-2x=0 },Q={x| x2+2x=0 },则P∪Q= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下给出对程序框图的几种说法:
①任何一个程序框图都必须有起止框;②输入框只能紧接开始框,输出框只能紧接结束框;③判断框是唯一具有超出一个退出点的符号;④对于一个问题的算法来说,其程序框图判断框内的条件的表述方法是唯一的.
其中正确说法的个数是__________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化.老师讲课开始时学生的兴趣激增,接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.该小组发现注意力指标
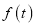 与上课时刻第
与上课时刻第  分钟末的关系如下
分钟末的关系如下 设上课开始时,
设上课开始时, :
: .若上课后第
.若上课后第 分钟末时的注意力指标为
分钟末时的注意力指标为 .
.(1)求
 的值;
的值;(2)上课后第
 分钟末和下课前
分钟末和下课前 分钟末比较,哪个时刻注意力更集中?
分钟末比较,哪个时刻注意力更集中?(3)在一节课中,学生的注意力指标至少达到
 的时间能保持多长?
的时间能保持多长? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 和
和 分别是
分别是 上的奇函数和偶函数,且
上的奇函数和偶函数,且 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(Ⅰ)求函数
 的解析式;
的解析式;(Ⅱ)当
 时,分别求出曲线
时,分别求出曲线 和
和 切线斜率的最小值;
切线斜率的最小值;(Ⅲ)设
 ,证明:当
,证明:当 时,曲线
时,曲线 在曲线
在曲线 和
和 之间,且相互之间没有公共点.
之间,且相互之间没有公共点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
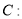
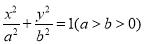 的两个焦点分别为
的两个焦点分别为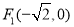 ,
,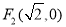 ,以椭圆短轴为直径的圆经过点
,以椭圆短轴为直径的圆经过点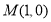 .
.(1)求椭圆
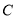 的方程;
的方程;(2)过点
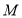 的直线
的直线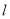 与椭圆
与椭圆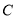 相交于
相交于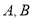 两点,设直线
两点,设直线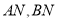 的斜率分别为
的斜率分别为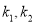 ,问
,问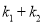 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.
相关试题

