【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
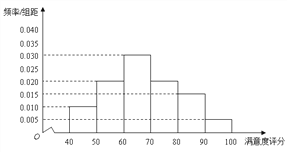
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由
参考答案:
【答案】(1) B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散。(2) A地区用户的满意度等级为不满意的概率大
【解析】试题分析:(I)根据分布表的数据,画出频率直方图,图形集中的分散程度小,矩形高的多,平均值高。(II)计算得出CA表示事件:“A地区用户的满意度等级为不满意”,CB表示事件:“B地区用户的满意度等级为不满意”,P(CA),P(CB),即可判断不满意的情况
解析:
(Ⅰ)
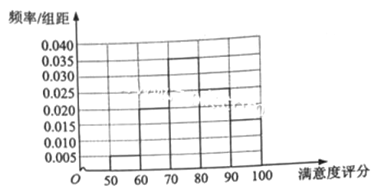
通过两地区用户满意度评分的频率分布直方图可以看出,B地区用户满意度评分的平均值高于A地区用户满意度评分的平均值;B地区用户满意度评分比较集中,而A地区用户满意度评分比较分散。
(Ⅱ)A地区用户的满意度等级为不满意的概率大。
记![]() 表示事件:“A地区用户的满意度等级为不满意”; 记
表示事件:“A地区用户的满意度等级为不满意”; 记![]() 表示事件:“B地区用户的满意度等级为不满意”。
表示事件:“B地区用户的满意度等级为不满意”。
由直方图得![]() 的估计值为
的估计值为![]()
![]() 的估计值为
的估计值为![]()
所以A地区用户的满意度等级为不满意的概率大。
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)分析,你认为选派哪位学生参加合适?请说明理由
参考公式:

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
-
科目: 来源: 题型:
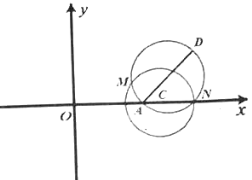
查看答案和解析>>【题目】如图,圆
 的圆心在
的圆心在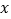 轴上,且过点
轴上,且过点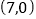 ,
,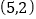 .
.
(1)求圆
 的方程;
的方程;(2)直线
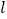 :
: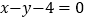 与
与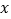 轴交于点
轴交于点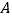 ,点
,点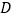 为直线
为直线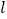 上位于第一象限内的一点,以
上位于第一象限内的一点,以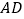 为直径的圆与圆
为直径的圆与圆 相交于点
相交于点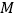 ,
,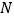 .若直线
.若直线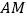 的斜率为-2,求
的斜率为-2,求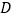 点坐标.
点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 ,
, 满足
满足 ,数列
,数列 前
前 项和为
项和为 .
.(1)若数列
 是首项为正数,公比为
是首项为正数,公比为 的等比数列.
的等比数列.①求证:数列
 为等比数列;
为等比数列;②若
 对任意
对任意 恒成立,求
恒成立,求 的值;
的值;(2)已知
 为递增数列,即
为递增数列,即 .若对任意
.若对任意 ,数列
,数列 中都存在一项
中都存在一项 使得
使得 ,求证:数列
,求证:数列 为等差数列.
为等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:
时间
星期一
星期二
星期三
星期四
星期五
星期六
星期日
车流量x(万辆)
1
2
3
4
5
6
7
PM2.5的浓度y(微克/立方米)
28
30
35
41
49
56
62
(Ⅰ)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是
 ,其中
,其中 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,若输出的结果为
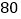 ,则判断框内应填入( )
,则判断框内应填入( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

