【题目】
等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD 所在的平面和平面ABEF互相垂直.
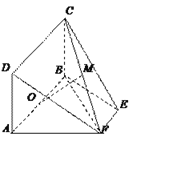
(1)求证:AF⊥平面CBF;
(2)设FC的中点为M,求证:OM∥平面DAF;
(3)求三棱锥C-BEF的体积.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)要证线与面垂直,需先证明直线![]() 垂直于平面内的两条相交直线,因为矩形
垂直于平面内的两条相交直线,因为矩形![]() 所在的平面和平面
所在的平面和平面![]() 互相垂直,所以
互相垂直,所以![]() 垂直于平面
垂直于平面![]() ,从而
,从而![]() 垂直于
垂直于![]() ,依题意,
,依题意,![]() 垂直于
垂直于![]() ,从而命题得证;(2)取
,从而命题得证;(2)取![]() 的中点为
的中点为![]() ,由三角形中位线定理,
,由三角形中位线定理,![]() 平行
平行![]() 且等于
且等于![]() 的一半,而
的一半,而![]() 也是如此,从而
也是如此,从而![]() 平行且等于
平行且等于![]() ,四边形
,四边形![]() 为平行四边形,所以
为平行四边形,所以![]() 平行于
平行于![]() ,由线面平行的判定定理即可得证
,由线面平行的判定定理即可得证![]() 平行于平面
平行于平面![]() ;(3)先计算底面三角形
;(3)先计算底面三角形![]() 的面积,在等腰梯形
的面积,在等腰梯形![]() 中,可得此三角形的高为
中,可得此三角形的高为![]() ,底
,底![]() 为1,再计算三棱锥
为1,再计算三棱锥![]() 的高,即为
的高,即为![]() ,最后由三棱锥体积计算公式计算即可.
,最后由三棱锥体积计算公式计算即可.
试题解析:(1) ∵平面ABCD⊥平面ABEF,CB⊥AB,
平面ABCD∩平面ABEF=AB,∴CB⊥平面ABEF,
∵AF平面ABEF,∴AF⊥CB.
又∵AF⊥BF,BF∩BC=B,BF,BC平面CBF.
∴AF⊥平面CBF.
(2) 设DF的中点为N,则MN∥CD,MN=CD,
AO∥CD,AO=CD,则MN∥AO,MN=AO,
∴四边形MNAO是平行四边形,∴OM∥AN.
又AN平面DAF,OM平面DAF,∴OM∥平面DAF.
(3) 过点E作EH⊥AB于H,则∠EBH=60°,
所以EH=![]() ,EF=AB-2HB=1,故S△BEF=×1×
,EF=AB-2HB=1,故S△BEF=×1×![]() =
=![]() ,VC-BEF=×S△BEF×BC=
,VC-BEF=×S△BEF×BC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
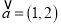 ,
, 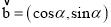 .设
.设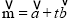 (t为实数).
(t为实数).(Ⅰ)若
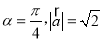 ,求当
,求当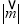 取最小值时实数t的值;
取最小值时实数t的值;(Ⅱ)若
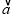 ⊥
⊥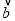 ,问:是否存在实数t,使得向量
,问:是否存在实数t,使得向量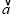 -
-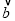 和向量
和向量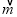 的夹角为
的夹角为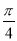 ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为
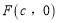 的椭圆
的椭圆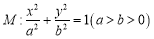 过点
过点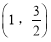 ,且椭圆
,且椭圆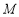 关于直线
关于直线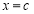 对称的图形过坐标原点.
对称的图形过坐标原点.(1)求椭圆
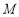 的方程;
的方程;(2)过点
 且不垂直于
且不垂直于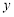 轴的直线与椭圆
轴的直线与椭圆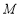 交于
交于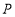 ,
,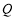 两点,点
两点,点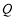 关于
关于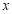 轴的对称点为
轴的对称点为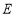 ,证明:直线
,证明:直线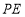 与
与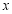 轴的交点为
轴的交点为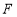 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一块圆心角为120°,半径为20cm的扇形钢片裁出一块矩形钢片,如图有两种裁法:使矩形一边在扇形的一条半径OA上,或者让矩形一边与弦AB平行,试问哪种裁法能使截得的矩形钢片面积最大?并求出这个最大值.

-
科目: 来源: 题型:
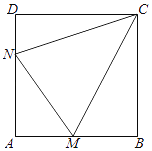
查看答案和解析>>【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax3-
 x2+1(xR),其中a>0.
x2+1(xR),其中a>0. (1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若在区间
 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为
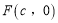 的椭圆
的椭圆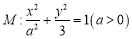 关于直线
关于直线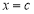 对称的图形过坐标原点.
对称的图形过坐标原点.(1)求椭圆
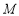 的方程;
的方程;(2)过点
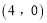 且不垂直于
且不垂直于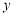 轴的直线与椭圆
轴的直线与椭圆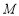 交于
交于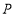 ,
,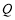 两点,点
两点,点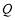 关于
关于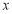 轴的对称点为
轴的对称点为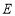 ,证明:直线
,证明:直线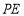 与
与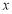 轴的交点为
轴的交点为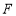 .
.
相关试题

