【题目】设函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;![]() 函数
函数![]() 在其定义域上存在极值.
在其定义域上存在极值.
(1)若![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)如果“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)原命题等价于![]() 对
对![]() 恒成立
恒成立![]()
![]() 对
对![]() 恒成立
恒成立![]()
![]()
![]()
![]() 的取值范围为
的取值范围为![]() ;(2)求导得
;(2)求导得![]()
若![]() 在定义域单调递增,在其定义域上不存在极值,不符合题意;若
在定义域单调递增,在其定义域上不存在极值,不符合题意;若![]() ,则
,则![]() ,由
,由![]()
![]()
![]()
![]() 若
若![]() 为真命题,则
为真命题,则![]() .由已知可得
.由已知可得![]() 与
与![]() 一真一假
一真一假![]()
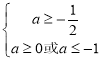 或
或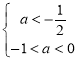
![]()
![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.
试题解析: (1)因为![]() ,
,
所以![]() 对
对![]() 恒成立,....................1分
恒成立,....................1分
因为![]() ,所以
,所以![]() 对
对![]() 恒成立,..............3分
恒成立,..............3分
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() ..............4分
..............4分
(2)对于![]() ,..............5分
,..............5分
若![]() 在定义域单调递增,在其定义域上不存在极值,不符合题意;........6分
在定义域单调递增,在其定义域上不存在极值,不符合题意;........6分
若![]() ,则
,则![]() ,由
,由![]() ,解得
,解得![]() ,
,
所以,若![]() 为真命题,则
为真命题,则![]() ,..............8分
,..............8分
因为“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题,所以命题
”为假命题,所以命题![]() 与
与![]() 一真一假,
一真一假,
①![]() 真
真![]() 假时,
假时,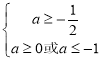 ,解得
,解得![]() ,
,
②![]() 假
假![]() 真时,
真时,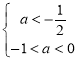 ,解得
,解得![]()
综上所述,![]() 的取值范围为
的取值范围为![]() ...................12分
...................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|ax2-2x+2=0},集合B={y|y2-3y+2=0},如果AB,求实数a的取值集合..
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是定义在(0,+∞)上的递增函数,对于任意的x>0,y>0,都有f(xy)=f(x)+f(y),且满足f(2)=1.
(1)求f(1),f(4)的值;
(2)求满足f(2)+f(x-3)≤2的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数
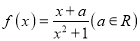 是奇函数,函数
是奇函数,函数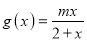 的定义域为
的定义域为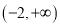 .
.(1)求
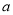 的值;
的值;(2)若
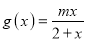 在
在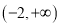 上单调递减,根据单调性的定义求实数
上单调递减,根据单调性的定义求实数 的取值范围;
的取值范围;(3)在(2)的条件下,若函数
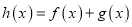 在区间
在区间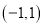 上有且仅有两个不同的零点,求实数
上有且仅有两个不同的零点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(Ⅰ)当0≤x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=xv(x)可以达到最大,并求出最大值.(精确到1辆/小时).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的通项公式是an=
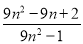 .
.(1) 判断
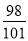 是不是数列{an}中的一项;
是不是数列{an}中的一项;(2) 试判断数列{an}中的项是否都在区间(0,1)内;
(3) 在区间
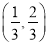 内有无数列{an}中的项?若有,是第几项?若没有,请说明理由.
内有无数列{an}中的项?若有,是第几项?若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-1,g(x)=

(1)求f[g(2)]和g[f(2)]的值;
(2)求f[g(x)]和g[f(x)]的表达式.
相关试题

