Question

【题目】已知函数.

（1）若曲线在处的切线的斜率为3，求实数的值；

（2）若函数在区间上存在极小值，求实数的取值范围；

（3）如果的解集中只有一个整数，求实数的取值范围.

Answer 1

【答案】（1）（2）（3）

【解析】

（1）先求出，利用可求.

（2）因函数在区间上存在极小值，故在上有解，利用求根公式求出的较大的根，它在区间中，从而得到的取值范围，

（3）利用导数可得当时，为上的增函数，而，故无整数解；当时，因在上有两个不同的解且，所以在上为增函数，在上为减函数，在上为增函数，结合可以得到，从而得到的取值范围.

（1）由题意，，

由题意知，，所以，解得.

（2）令，所以，所以（舍负），

因为函数在上存在极小值，所以，

解之得，

经检验，当时，符合题意，

所以.

（3）①当，即时，恒成立，

在上为增函数，.

所以当时，，所以当时，，所以无整数解；

②当，即或时，

若，则，同①可得无整数解；

若，即在上有两个不同的解且，

当时，，在上为增函数；

当时，，在上为减函数；

当时，，在上为增函数，

而，所以在上无解，故在上只有一个整数解，

故，即，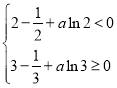

解得，

综上，.