【题目】有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P(万元)和Q(万元),它们与投入资金x(万元)的关系有经验公式:P=![]() ,Q=
,Q=![]()
![]() .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得的最大利润是多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得的最大利润是多少?
参考答案:
【答案】详见解析.
【解析】试题分析: 设对甲种商品投资x万元,则对乙种商品投资(3-x)万元,总利润为y万元,
根据总利润=甲的利润+乙的利润,可得函数解析式,利用换元法转化为二次函数,用配方法求出最值.
试题解析:
设对甲种商品投资x万元,则对乙种商品投资(3-x)万元,总利润为y万元,
根据题意得y=![]() x+
x+![]()
![]() (0≤x≤3).令
(0≤x≤3).令![]() =t,则x=3-t2,0≤t≤
=t,则x=3-t2,0≤t≤![]() .
.
所以y=![]()
![]() +
+![]() t=-
t=-![]()
![]() 2+
2+![]() ,t∈[0,
,t∈[0,![]() ].
].
当t=![]() 时,ymax=
时,ymax=![]() ,此时x=0.75,3-x=2.25.
,此时x=0.75,3-x=2.25.
由此可知,为获得最大利润,对甲、乙两种商品的资金投入分别应为0.75万元和2.25万元,能获得的最大利润为1.05万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
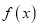 的定义域为
的定义域为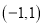 ,对任意实数
,对任意实数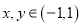 ,都有
,都有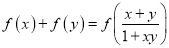 .
.(1)若
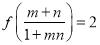 ,
, 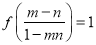 ,且
,且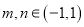 ,求
,求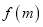 ,
, 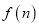 的值;
的值;(2)若
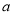 为常数,函数
为常数,函数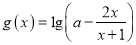 是奇函数,
是奇函数,①验证函数
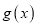 满足题中的条件;
满足题中的条件;②若函数
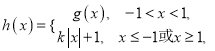 求函数
求函数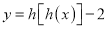 的零点个数.
的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
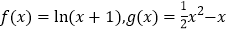 .
.(Ⅰ)求过点
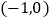 且与曲线
且与曲线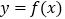 相切的直线方程;
相切的直线方程;(Ⅱ)设
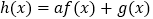 ,其中
,其中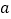 为非零实数,若
为非零实数,若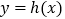 有两个极值点
有两个极值点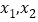 ,且
,且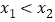 ,求证:
,求证: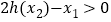 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】做一个无盖的圆柱形水桶,若要使其体积是
 ,且用料最省,则圆柱的底面半径为__________.
,且用料最省,则圆柱的底面半径为__________. -
科目: 来源: 题型:
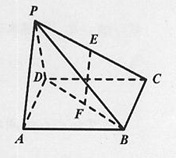
查看答案和解析>>【题目】如图,在四棱锥
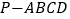 中,底面
中,底面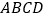 是边长为2的正方形,
是边长为2的正方形,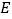 ,
,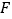 分别为
分别为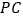 ,
,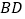 的中点,平面
的中点,平面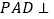 平面
平面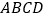 ,且
,且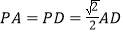 .
.
(1)求证:
 平面
平面 ;
;(2)求三棱锥
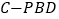 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲
82
82
79
95
87
乙
95
75
80
90
85
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
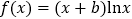 ,已知曲线
,已知曲线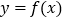 在点
在点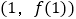 处的切线与直线
处的切线与直线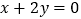 垂直.
垂直.(1)求
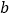 的值;
的值;(2)若函数
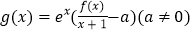 ,且
,且 在区间
在区间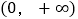 上是单调函数,求实数
上是单调函数,求实数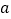 的取值范围.
的取值范围.
相关试题

