【题目】设椭圆![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() 直线
直线![]() ,且直线
,且直线![]() 分别与椭圆
分别与椭圆![]() 相交于
相交于![]() 两点和
两点和![]() 两点.
两点.
(Ⅰ)若![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,且直线
的左、右焦点,且直线![]() 轴,求四边形
轴,求四边形![]() 的面积;
的面积;
(Ⅱ)若直线![]() 的斜率存在且不为0,四边形
的斜率存在且不为0,四边形![]() 为平行四边形,求证:
为平行四边形,求证:![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,判断四边形![]() 能否为矩形,说明理由.
能否为矩形,说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)证明见解析;(Ⅲ)不能,证明见解析
;(Ⅱ)证明见解析;(Ⅲ)不能,证明见解析
【解析】
(Ⅰ)计算得到故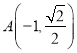 ,
,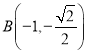 ,
,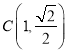 ,
,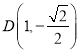 ,计算得到面积.
,计算得到面积.
(Ⅱ) 设![]() 为
为![]() ,联立方程得到
,联立方程得到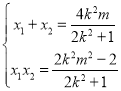 ,计算
,计算![]() ,同理
,同理![]() ,根据
,根据![]() 得到
得到![]() ,得到证明.
,得到证明.
(Ⅲ) 设![]() 中点为
中点为![]() ,根据点差法得到
,根据点差法得到![]() ,同理
,同理![]() ,故
,故![]() ,得到结论.
,得到结论.
(Ⅰ)![]() ,
,![]() ,故
,故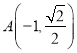 ,
,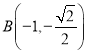 ,
,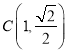 ,
,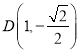 .
.
故四边形![]() 的面积为
的面积为![]() .
.
(Ⅱ)设![]() 为
为![]() ,则
,则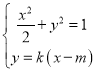 ,故
,故![]() ,
,
设![]() ,
,![]() ,故
,故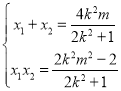 ,
,
![]() ,
,
同理可得![]() ,
,
![]() ,故
,故![]() ,
,
即![]() ,
,![]() ,故
,故![]() .
.
(Ⅲ)设![]() 中点为
中点为![]() ,则
,则![]() ,
,![]() ,
,
相减得到![]() ,即
,即![]() ,
,
同理可得:![]() 的中点
的中点![]() ,满足
,满足![]() ,
,
故![]() ,故四边形
,故四边形![]() 不能为矩形.
不能为矩形.

