【题目】已知函数f(x)=|x|(x﹣a),a为实数.
(1)若函数f(x)为奇函数,求实数a的值;
(2)若函数f(x)在[0,2]为增函数,求实数a的取值范围;
(3)是否存在实数a(a<0),使得f(x)在闭区间![]() 上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
参考答案:
【答案】(1) a=0.(2)a≤0(3)a=﹣3.
【解析】试题分析:(1)因为f(x)为奇函数,所以f(﹣x)=﹣f(x),根据函数解析式,化简式子得2a|x|=0对任意x∈R恒成立,求得![]() ;(2)当
;(2)当![]() 时,f(x)=|x|(x﹣a)可去掉绝对值号得f(x)=x(x﹣a),其对称轴为
时,f(x)=|x|(x﹣a)可去掉绝对值号得f(x)=x(x﹣a),其对称轴为![]() ,要使函数f(x)在[0,2]上单调递增,由二次函数的图像可得
,要使函数f(x)在[0,2]上单调递增,由二次函数的图像可得![]() ,求
,求![]() 的范围。(3)当
的范围。(3)当![]() 时,
时, ![]() 的解析式去掉绝对值号可得
的解析式去掉绝对值号可得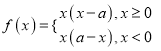 ,因为f(x)在闭区间
,因为f(x)在闭区间![]() 上的最大值为2,由特殊值
上的最大值为2,由特殊值![]() ,限定
,限定![]() 的范围,因为函数
的范围,因为函数![]() 的对称轴为
的对称轴为![]() ,因为a<0,所以函数
,因为a<0,所以函数![]() 在(0,+∞)上递增,所以
在(0,+∞)上递增,所以![]() ,所以
,所以![]() 必在区间[﹣1,0]上取最大值2,讨论函数
必在区间[﹣1,0]上取最大值2,讨论函数![]() 在[﹣1,0]上的单调性,最大值等于2,可求实数
在[﹣1,0]上的单调性,最大值等于2,可求实数![]() 的值。
的值。
试题解析:(1)因为奇函数f(x)定义域为R,
所以f(﹣x)=﹣f(x)对任意x∈R恒成立,
即|﹣x|(﹣x﹣a)=﹣|x|(x﹣a),即|x|(﹣x﹣a+x﹣a)=0,
即2a|x|=0对任意x∈R恒成立,
所以a=0.
(2)因为x∈[0,2],所以f(x)=x(x﹣a),
显然二次函数的对称轴为![]() ,由于函数f(x)在[0,2]上单调递增,
,由于函数f(x)在[0,2]上单调递增,
所以![]() ,
,
即a≤0(若分a<0,a=0,a>0三种情况讨论即可)
(3)∵a<0,![]() ,
,
∴f(﹣1)=﹣1﹣a≤2,∴﹣a≤3(先用特殊值约束范围)
∴![]() ,f(x)在(0,+∞)上递增,
,f(x)在(0,+∞)上递增,
∴f(x)必在区间[﹣1,0]上取最大值2.
当![]() ,即a<﹣2时,则f(﹣1)=2,a=﹣3成立
,即a<﹣2时,则f(﹣1)=2,a=﹣3成立
当![]() ,即0>a≥﹣2时,
,即0>a≥﹣2时,![]() ,则
,则![]() (舍)
(舍)
综上,a=﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
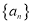 的前
的前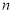 项和为
项和为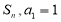 ,且对任意正整数
,且对任意正整数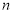 ,满足
,满足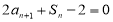 .
.(1)求数列
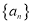 的通项公式.
的通项公式.(2)设
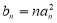 ,求数列
,求数列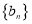 的前
的前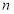 项和
项和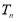 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
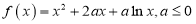 .
.(1)若当
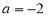 时,求
时,求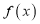 的单调区间;
的单调区间;(2)若
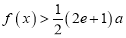 ,求
,求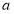 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式组

(1) 若k=1,求不等式组的解集;
(2) 若不等式组的整数解的集合为{-2},求实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2-2|x|-1,-3≤x≤3.
(1)证明:f(x)是偶函数;
(2)指出函数f(x)的单调区间;
(3)求函数的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={x|ax2-2x+2=0},集合B={y|y2-3y+2=0},如果AB,求实数a的取值集合..
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是定义在(0,+∞)上的递增函数,对于任意的x>0,y>0,都有f(xy)=f(x)+f(y),且满足f(2)=1.
(1)求f(1),f(4)的值;
(2)求满足f(2)+f(x-3)≤2的x的取值范围.
相关试题

