【题目】定义域为R的偶函数f(x)满足对x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,则a的取值范围是 .
参考答案:
【答案】(0, ![]() )
)
【解析】解:∵f(x+2)=f(x)﹣f(1),
且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
又f(﹣1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2 ,
函数的图象为开口向下、顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点.
∵f(x)≤0,∴g(x)≤0,可得0<a<1,
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=﹣2,
即loga3>﹣2,∴3< ![]() ,解得-
,解得- ![]() <a<
<a< ![]() ,又0<a<1,∴0<a<
,又0<a<1,∴0<a< ![]() ,
,
故答案为:(0, ![]() ).
).
令x=﹣1,求出f(1),可得函数f(x)的周期为2,当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,画出图形,根据函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,利用数形结合的方法进行求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个水轮的半径为4米,水轮圆心
 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点
距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点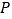 从水中浮现(图中点
从水中浮现(图中点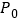 )开始计算时间.
)开始计算时间.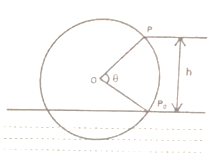
(1)将点
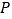 距离水面的高度
距离水面的高度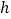 (米)表示为时间
(米)表示为时间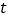 (秒)的函数;
(秒)的函数;(2)在水轮旋转一圈内,有多长时间点
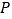 离开水面?
离开水面? -
科目: 来源: 题型:
查看答案和解析>>【题目】棱台
 的三视图与直观图如图所示.
的三视图与直观图如图所示.
(1)求证:平面
 平面
平面 ;
;(2)在线段
 上是否存在一点
上是否存在一点 ,使
,使 与平面
与平面 所成的角的正弦值为
所成的角的正弦值为 ?若存在,指出点
?若存在,指出点 的位置;若不存在,说明理由.
的位置;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为常数,函数
为常数,函数 .
.(1)当
 时,求关于
时,求关于 的不等式
的不等式 的解集;
的解集;(2)当
 时,若函数
时,若函数 在
在 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;(3)当
 时,对于给定的
时,对于给定的 ,且
,且 ,
, ,证明:关于
,证明:关于 的方程
的方程 在区间
在区间 内有一个实根.
内有一个实根. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列几个命题
①奇函数的图象一定通过原点
②函数
 是偶函数,但不是奇函数
是偶函数,但不是奇函数③函数f(x)=ax﹣1+3的图象一定过定点P,则P点的坐标是(1,4)
④若f(x+1)为偶函数,则有f(x+1)=f(﹣x﹣1)
⑤若函数
 在R上的增函数,则实数a的取值范围为[4, 8)
在R上的增函数,则实数a的取值范围为[4, 8)其中正确的命题序号为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点为
的焦点为 ,过点
,过点 的直线
的直线 交抛物线
交抛物线 于
于 (
(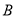 位于第一象限)两点.
位于第一象限)两点.(1)若直线
 的斜率为
的斜率为 ,过点
,过点 分别作直线
分别作直线 的垂线,垂足分别为
的垂线,垂足分别为 ,求四边形
,求四边形 的面积;
的面积; (2)若
 ,求直线
,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某商场旅游鞋的日销售情况,现抽取部分顾客购鞋的尺码,将所得数据绘成如图所示频率分布直方图,已知图中从左到右前三组的频率之比为1:2:3,第二组的频数为10.

(1)用频率估计概率,求尺码落在区间(37.5,43.5]概率约是多少?
(2)从尺码落在区间(37.5,39.5](43.5,45.5]顾客中任意选取两人,记在区间(43.5,45.5]的人数为X,求X的分布列及数学期望EX.
相关试题

