【题目】为阻隔新冠肺炎病毒，多地进行封城.封城一段时间后，有的人情绪波动不大，反应一般；也有的人情绪波动大，反应强烈.某社区为了解民众心理反应，随机调查了100位居民，得到数据如下表：

反应强烈

反应一般

合计

男

20

20

40

女

45

15

60

合计

65

35

100

（1）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若从该社区的男性居民中随机抽取3位，记其中反应强烈的人数为X，求随机变量X的分布列和数学期望；

（2）根据调查数据，能否在犯错的概率不超过的前提下认为“反应强烈”与性别有关，并说明理由.

参考数据：

k

（参考公式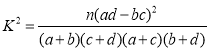：，其中）

【答案】（1）答案见解析，；（2）能，理由见解析.

【解析】

（1）从表格中的数据中先求出男性居民“反应强烈”的概率，而X服从二项分布，然后直接利用二项分布的概率公式，求每一个所对应的概率，再列随机变量X的分布列即可；

（2）直接利用公式求解，然后与临界值5.024比较即可

解：（1）由已知得男性居民“反应强烈”的概率为，并且，

所以.

其分布列如下

X

0

1

2

3

P

所以，（或）.

（2）因为

所以能在犯错的概率不超过的前提下认为“反应强烈”与性别有关.

关闭