【题目】【2017广东佛山二模】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)  .
.
【解析】试题分析:(1)先根据焦距确定焦点坐标,再根据对称性得![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线为
的交点所在的直线为![]() ,即得一个交点为
,即得一个交点为![]() ,代入椭圆方程,结合
,代入椭圆方程,结合![]() 可解得
可解得![]() ,
, ![]() ;(2)先设直线
;(2)先设直线![]() :
: ![]() ,由直线
,由直线![]() 与抛物线
与抛物线![]() 无公共点,利用判别式小于零得
无公共点,利用判别式小于零得![]() .由弦长公式可求底边AB长,利用点
.由弦长公式可求底边AB长,利用点![]() 到直线
到直线![]() 距离可得高,代入面积公式可得
距离可得高,代入面积公式可得![]() ,根据对勾函数确定其值域.
,根据对勾函数确定其值域.
试题解析:(Ⅰ)依题意得![]() ,则
,则![]() ,
, ![]() .
.
所以椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() ,
,
于是![]()
![]() ,从而
,从而![]() .
.
又![]() ,解得
,解得![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)依题意,直线![]() 的斜率不为0,设直线
的斜率不为0,设直线![]() :
: ![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() ,由
,由![]() 得
得![]() .
.
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]()
![]()
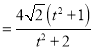 ,
,
![]() 到直线
到直线![]() 距离
距离![]() ,
,
故![]()
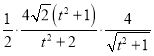
![]() ,
,
令![]() ,则
,则![]()

 ,
,
所以三边形![]() 的面积的取值范围为
的面积的取值范围为 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017河北唐山三模】已知函数
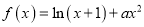 ,
, 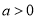 .
.(1)讨论函数
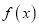 的单调性;
的单调性;(2)若函数
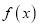 在区间
在区间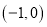 有唯一零点
有唯一零点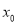 ,证明:
,证明: 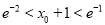 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足
 =
=  +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017四川宜宾二诊】已知函数
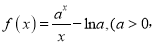 且
且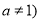 .
.(I)若
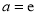 ,求函数
,求函数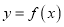 的单调区间;(其中
的单调区间;(其中 是自然对数的底数)
是自然对数的底数)(II)设函数
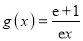 ,当
,当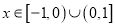 时,曲线
时,曲线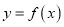 与
与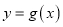 有两个交点,求
有两个交点,求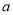 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017福建三明5月质检】已知直线
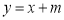 与抛物线
与抛物线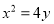 相切,且与
相切,且与 轴的交点为
轴的交点为 ,点
,点 .若动点
.若动点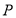 与两定点
与两定点 所构成三角形的周长为6.
所构成三角形的周长为6.(Ⅰ) 求动点
 的轨迹
的轨迹 的方程;
的方程;(Ⅱ) 设斜率为
 的直线
的直线 交曲线
交曲线 于
于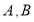 两点,当
两点,当 ,且
,且 位于直线
位于直线 的两侧时,证明:
的两侧时,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣
 ax2+x,a∈R.
ax2+x,a∈R.
(1)若f(1)=0,求函数f(x)的最大值;
(2)令g(x)=f(x)﹣(ax﹣1),求函数g(x)的单调区间;
(3)若a=﹣2,正实数x1 , x2满足f(x1)+f(x2)+x1x2=0,证明x1+x2≥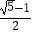 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为 .
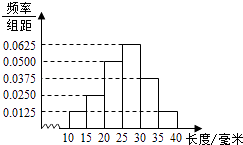
相关试题

