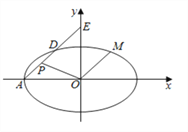
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若过![]() 点作直线
点作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)椭圆![]() 的标准方程为
的标准方程为![]() ;(2)定点
;(2)定点![]() 的坐标为
的坐标为![]() .(3)当
.(3)当![]() 时,
时, ![]() 的最小值为
的最小值为![]() .
.
【解析】试题分析:(1)由椭圆的离心率![]() ,左顶点为
,左顶点为![]() 易得结论;(2)直线
易得结论;(2)直线![]() 的方程为
的方程为![]() ,联立椭圆方程消去y,由根与系数的关系,求出点P坐标,根据题意
,联立椭圆方程消去y,由根与系数的关系,求出点P坐标,根据题意![]() ,则结论易得;(3)设
,则结论易得;(3)设![]() 的方程可设为
的方程可设为![]() ,联立椭圆方程,求出点M坐标,
,联立椭圆方程,求出点M坐标, ![]() =
=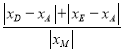 ,结合基本不等式求解即可.
,结合基本不等式求解即可.
试题解析:
(1) ![]() 椭圆
椭圆![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]()
![]() ,
,
![]() =
=![]() =
=![]()
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)直线![]() 的方程为
的方程为![]() ,
,
由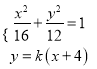 消元得
消元得![]() =
=![]()
![]() =
=![]() =
=![]()
当![]() 时,
时, ![]() =
= 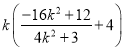 =
=![]()
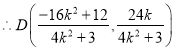 ,
,
![]() 点
点![]() 为
为![]() 的中点,
的中点,
![]() 的坐标为
的坐标为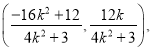
则![]() =
=![]()
直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() 点坐标为
点坐标为![]()
假设存在定点![]() 使得
使得![]() ,
,
则![]() ,即
,即![]() =
=![]() 恒成立,
恒成立,
![]() 恒成立,
恒成立,
![]() ,即
,即![]() ,
,
![]() 定点
定点![]() 的坐标为
的坐标为![]()
(3) ![]() ,
,
![]() 的方程可设为
的方程可设为![]() .
.
由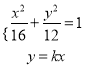 ,得
,得![]() 点的横坐标为
点的横坐标为![]() =
=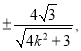
由![]() ,
,
得![]() =
=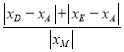 =
=![]() =
=![]() =
=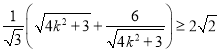 ,
,
当且仅当![]() =
=![]() 即
即![]() 时取“=”,
时取“=”,
![]() 当
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用
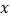 (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人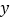 (万元)的数据如下表:
(万元)的数据如下表:年份
2013年
2014年
2015年
2016年
2017年
促销费用
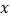
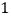
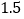
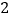
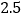
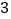
销售收入
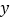
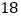
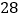
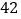
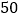
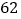
(1)请根据上表提供的数据,用最小二乘法求出/span>
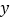 关于
关于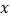 的线性回归方
的线性回归方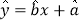 ;
;(2)2018年度该店铺预测销售收人至少达到
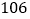 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?参考公式:
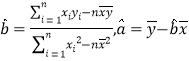
参考数据:
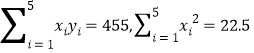
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
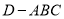 中,已知
中,已知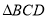 是正三角形,
是正三角形,  平面
平面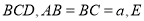 为
为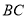 的中点,
的中点, 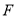 在棱
在棱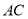 上,且
上,且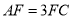 .
.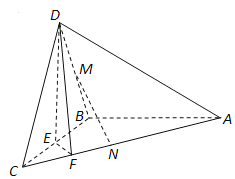
(1)求三棱锥
 的体积;
的体积;(2)求证:
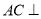 平面
平面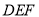 ;
;(3)若
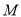 为
为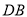 中点,
中点,  在棱
在棱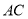 上,且
上,且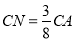 ,求证:
,求证: 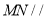 平面
平面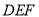 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:
 及其上一点A(2,4)
及其上一点A(2,4)
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得
 ,求实数t的取值范围。
,求实数t的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车是城市交通的一道亮丽的风景,给人们短距离出行带来了很大的方便.某校”单车社团”对
 市年龄在
市年龄在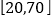 岁骑过共享单车的人群随机抽取
岁骑过共享单车的人群随机抽取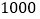 人调查,骑行者的年龄情况如下图显示。
人调查,骑行者的年龄情况如下图显示。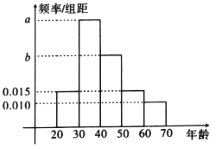
(1)已知
 年龄段的骑行人数是
年龄段的骑行人数是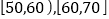 两个年龄段的人数之和,请估计骑过共享单车人群的年齡的中位数;
两个年龄段的人数之和,请估计骑过共享单车人群的年齡的中位数;(2)从
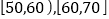 两个年龄段骑过共享单车的人中按
两个年龄段骑过共享单车的人中按 的比例用分层抽样的方法抽取
的比例用分层抽样的方法抽取 人,从中任选
人,从中任选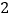 人,求两人都在
人,求两人都在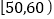 )的概率.
)的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 与抛物线
与抛物线 有相同的焦点
有相同的焦点 为原点,点
为原点,点 是准线上一动点,点
是准线上一动点,点 在抛物线上,且
在抛物线上,且 ,则
,则 的最小值为__________.
的最小值为__________.
相关试题

