【题目】已知函数f(x)=4x2﹣4ax+a2﹣2a+2在区间[0,2]上有最小值3,求实数a的值.
参考答案:
【答案】![]() 或
或![]()
【解析】试题分析:确定二次函数的最值,首先要确定其在定义域上的单调性,本题中二次函数对称轴为![]() ,因此首先讨论对称轴位置的三种情况:
,因此首先讨论对称轴位置的三种情况:![]() ≤0,0<
≤0,0<![]() <2,
<2,![]() ≥2,从而确定其单调性,将最值转化为用a表示的关系式,求解a值
≥2,从而确定其单调性,将最值转化为用a表示的关系式,求解a值
试题解析:∵f(x)=4(x-![]() )2-2a+2,
)2-2a+2,
①当![]() ≤0,即a≤0时,函数f(x)在[0,2]上是增函数.
≤0,即a≤0时,函数f(x)在[0,2]上是增函数.
∴f(x)min=f(0)=a2-2a+2.
由a2-2a+2=3,得a=1±![]() .
.
∵a≤0,∴a=1-![]() .
.
②当0<![]() <2,即0<a<4时,
<2,即0<a<4时,
f(x)min=f(![]() )=-2a+2.
)=-2a+2.
由-2a+2=3,得a=-![]() (0,4),舍去.
(0,4),舍去.
③当![]() ≥2,即a≥4时,函数f(x)在[0,2]上是减函数,
≥2,即a≥4时,函数f(x)在[0,2]上是减函数,
f(x)min=f(2)=a2-10a+18.
由a2-10a+18=3,得a=5±![]() .
.
∵a≥4,∴a=5+![]() .
.
综上所述,a=1-![]() 或a=5+
或a=5+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
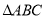 中, 角
中, 角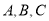 对边分别为
对边分别为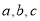 ,已知
,已知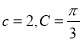 .
.(1)若
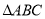 的面积等于
的面积等于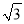 ,求
,求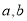 ;
;(2)若
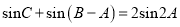 ,求
,求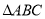 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
(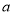 ﹥
﹥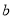 ﹥0)的离心率为
﹥0)的离心率为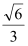 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为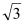 .
.(1)求椭圆
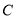 的方程;
的方程;(2)设直线
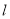 与椭圆
与椭圆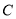 交于
交于 两点,坐标原点
两点,坐标原点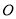 到直线
到直线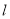 的距离为
的距离为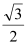 ,求
,求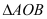 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
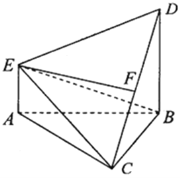
查看答案和解析>>【题目】如下图,在多面体
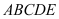 中,
中,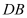 ⊥平面
⊥平面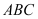 ,
, ,且
,且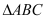 是边长为2的等边三角形,
是边长为2的等边三角形,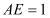 ,
,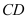 与平面
与平面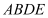 所成角的正弦值为
所成角的正弦值为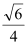 .
.
(1)若
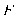 是线段
是线段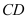 的中点,证明:
的中点,证明: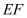 ⊥面
⊥面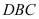 ;
;(2)求二面角
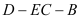 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若(
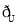 A)∩B=,求m的值.
A)∩B=,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,椭圆

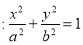 (
(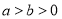 )的离心率是
)的离心率是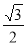 ,过点
,过点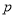 (
(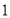 ,
, )的动直线
)的动直线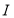 与椭圆相交于
与椭圆相交于 ,
,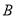 两点,当直线
两点,当直线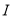 平行于
平行于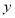 轴时,直线
轴时,直线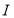 被椭圆
被椭圆 截得的线段长为
截得的线段长为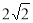 .
.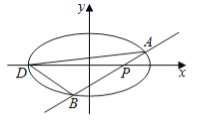
⑴求椭圆
 的方程:
的方程:⑵已知
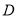 为椭圆的左端点,问: 是否存在直线
为椭圆的左端点,问: 是否存在直线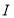 使得
使得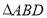 的面积为
的面积为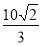 ?若不存在,说明理由,若存在,求出直线
?若不存在,说明理由,若存在,求出直线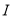 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是R上的偶函数,且当x>0时,函数的解析式为f(x)=
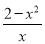 .
.(1)判断并证明f(x)在(0,+∞)上的单调性;
(2)求当x<0时,函数的解析式.
相关试题

