【题目】已知![]() ,若
,若![]() 的任何一条对称轴与
的任何一条对称轴与![]() 轴成交点的横坐标都不属于区间
轴成交点的横坐标都不属于区间![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】分析:由题意可得,![]() ≥3π﹣2π=π,求得
≥3π﹣2π=π,求得![]() <ω≤1,故排除A、D.检验当ω=
<ω≤1,故排除A、D.检验当ω=![]() 时,f(x)=
时,f(x)=![]() sin(
sin(![]() x﹣
x﹣![]() )满足条件,故排除B,从而得出结论.
)满足条件,故排除B,从而得出结论.
详解:f(x)=sinωx﹣cosωx=![]() sin(ωx﹣
sin(ωx﹣![]() )(ω>
)(ω>![]() ,x∈R),
,x∈R),
若f(x)的任何一条对称轴与x轴交点的横坐标都不属于区间(2π,3π),
则![]() ≥3π﹣2π=π,ω≤1,即
≥3π﹣2π=π,ω≤1,即![]() <ω≤1,故排除A、D.
<ω≤1,故排除A、D.
当ω=![]() 时,f(x)=
时,f(x)=![]() sin(
sin(![]() x﹣
x﹣![]() ),
),
令![]() x﹣
x﹣![]() =kπ+
=kπ+![]() ,求得 x=
,求得 x=![]() kπ+
kπ+![]() ,可得函数f(x)的图象的对称轴为 x=
,可得函数f(x)的图象的对称轴为 x=![]() kπ+
kπ+![]() ,k∈Z.
,k∈Z.
当k=1时,对称轴为 x=![]() <2π,当k=2时,对称轴为 x=
<2π,当k=2时,对称轴为 x=![]() =3π,
=3π,
满足条件:任何一条对称轴与x轴交点的横坐标都不属于区间(2π,3π),故排除B,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
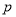 :实数
:实数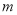 满足
满足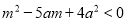 ,其中
,其中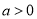 ;命题
;命题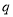 :方程
:方程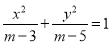 表示双曲线.
表示双曲线.(1)若
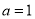 ,且
,且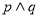 为真,求实数
为真,求实数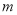 的取值范围;
的取值范围;(2)若
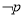 是
是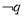 的充分不必要条件,求实数
的充分不必要条件,求实数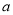 的取值范围.
的取值范围.【答案】(1)
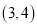 ;(2)
;(2)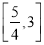 .
.【解析】试题分析:
先由命题解
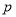 得
得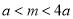 ;命题
;命题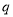 得
得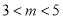 ,
,(1)当
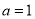 ,得命题
,得命题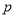 ,再由
,再由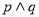 为真,得
为真,得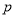 真且
真且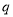 真,即可求解
真,即可求解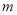 的取值范围.
的取值范围.(2)由
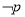 是
是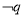 的充分不必要条件,则
的充分不必要条件,则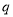 是
是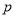 的充分必要条件,根据则
的充分必要条件,根据则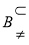
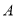 ,即可求解实数
,即可求解实数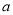 的取值范围.
的取值范围.试题解析:
命题
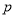 :由题得
:由题得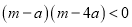 ,又
,又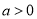 ,解得
,解得 ;
;命题
 :
: 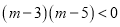 ,解得
,解得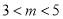 .
.(1)若
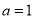 ,命题
,命题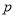 为真时,
为真时, 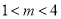 ,
,当
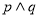 为真,则
为真,则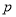 真且
真且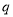 真,
真,∴
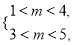 解得
解得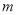 的取值范围是
的取值范围是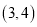 .
.(2)
 是
是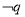 的充分不必要条件,则
的充分不必要条件,则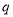 是
是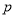 的充分必要条件,
的充分必要条件,设
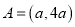 ,
, 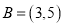 ,则
,则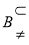
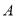 ;
;∴
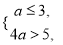 ∴实数
∴实数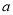 的取值范围是
的取值范围是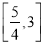 .
.【题型】解答题
【结束】
19【题目】已知抛物线顶点在原点,焦点在
 轴上,又知此抛物线上一点
轴上,又知此抛物线上一点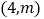 到焦点的距离为6.
到焦点的距离为6.(1)求此抛物线的方程;
(2)若此抛物线方程与直线
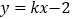 相交于不同的两点
相交于不同的两点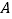 、
、 ,且
,且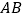 中点横坐标为2,求
中点横坐标为2,求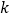 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从分别写有
 的
的 张卡片中随机抽取
张卡片中随机抽取 张,放回后再随机抽取
张,放回后再随机抽取 张,则抽得的第一张卡片,上的数不大于第二张卡片上的数的概率为( )
张,则抽得的第一张卡片,上的数不大于第二张卡片上的数的概率为( )A.
 B.
B.  C.
C.  D.
D. 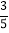
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为
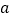 的正方体
的正方体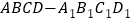 中,
中,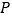 为
为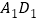 的中点,
的中点,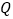 为
为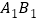 上任意一点,
上任意一点,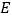 ,
,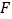 为
为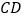 上任意两点,且
上任意两点,且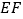 的长为定值,则下面的四个值中不为定值的是( )
的长为定值,则下面的四个值中不为定值的是( )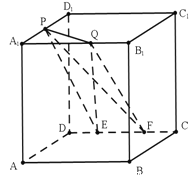
A. 点
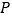 到平面
到平面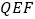 的距离B. 三棱锥
的距离B. 三棱锥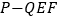 的体积
的体积C. 直线
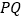 与平面
与平面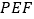 所成的角D. 二面角
所成的角D. 二面角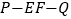 的大小
的大小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形, ,侧面
,侧面 底面
底面 ,
, ,
, ,
,  分别为
分别为 的中点,点
的中点,点 在线段
在线段 上.
上.
(Ⅰ)求证:
 平面
平面 ;
; (Ⅱ)如果直线
 与平面
与平面 所成的角和直线
所成的角和直线 与平面
与平面 所成的角相等,求
所成的角相等,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面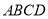 是平行四边形,
是平行四边形,  ,侧面
,侧面 底面
底面 ,
,  ,
,  ,
,  ,
,  分别为
分别为 ,
,  的中点,点
的中点,点 在线段
在线段 上.
上.
(1)求证:
 平面
平面 ;
;(2)若直线
 与平面
与平面 所成的角和直线
所成的角和直线 与平面
与平面 所成的角相等,求
所成的角相等,求 的值.
的值.【答案】(1)证明见解析;(2)
 .
.【解析】试题分析:
(Ⅰ)在平行四边形
 中,由条件可得
中,由条件可得 ,进而可得
,进而可得 。由侧面
。由侧面 底面
底面 ,得
,得 底面
底面 ,故得
,故得 ,所以可证得
,所以可证得 平面
平面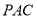 .(Ⅱ)先证明平面
.(Ⅱ)先证明平面 平面
平面 ,由面面平行的性质可得
,由面面平行的性质可得 平面
平面 .(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得
.(Ⅲ)建立空间直角坐标系,通过求出平面的法向量,根据线面角的向量公式可得 。
。试题解析:
(Ⅰ)证明:在平行四边形
 中,
中,∵
 ,
,  ,
,  ,
,∴
 ,
,∴
 ,
,∵
 ,
,  分别为
分别为 ,
,  的中点,
的中点,∴
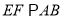 ,
,∴
 ,
,∵侧面
 底面
底面 ,且
,且 ,
,∴
 底面
底面 ,
,又
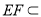 底面
底面 ,
,∴
 ,
,又
 ,
,  平面
平面 ,
,  平面
平面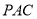 ,
,∴
 平面
平面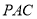 .
.(Ⅱ)证明:∵
 为
为 的中点,
的中点,  为
为 的中点,
的中点,∴
 ,
,又
 平面
平面 ,
,  平面
平面 ,
,∴
 平面
平面 ,
,同理
 平面
平面 ,
,又
 ,
,  平面
平面 ,
,  平面
平面 ,
,∴平面
 平面
平面 ,
,又
 平面
平面 ,
,∴
 平面
平面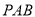 .
.(Ⅲ)解:由
 底面
底面 ,
,  ,可得
,可得 ,
,  ,
,  两两垂直,
两两垂直,建立如图空间直角坐标系
 ,
,
则
 ,
, 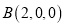 ,
,  ,
,  ,
,  ,
,  ,
,所以
 ,
,  ,
,  ,
,设
 ,则
,则 ,
,∴
 ,
,  ,
,易得平面
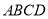 的法向量
的法向量 ,
,设平面
 的法向量为
的法向量为 ,则:
,则:由
 ,得
,得 ,
,令
 ,得
,得 ,
,∵直线
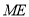 与平面
与平面 所成的角和此直线与平面
所成的角和此直线与平面 所成的角相等,
所成的角相等,∴
 ,即
,即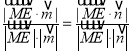 ,
,∴
 ,
,解得
 或
或 (舍去),
(舍去),故
 .
.点睛:用向量法确定空间中点的位置的方法
根据题意建立适当的空间直角坐标系,由条件确定有关点的坐标,运用共线向量用参数(参数的范围要事先确定)确定出未知点的坐标,根据向量的运算得到平面的法向量或直线的方向向量,根据所给的线面角(或二面角)的大小进行运算,进而求得参数的值,通过与事先确定的参数的范围进行比较,来判断参数的值是否符合题意,进而得出点是否存在的结论。
【题型】解答题
【结束】
21【题目】如图,椭圆
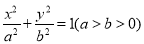 上的点到左焦点的距离最大值是
上的点到左焦点的距离最大值是 ,已知点
,已知点 在椭圆上,其中
在椭圆上,其中 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程;
(2)过原点且斜率为
 的直线交椭圆于
的直线交椭圆于 、
、 两点,其中
两点,其中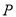 在第一象限,它在
在第一象限,它在 轴上的射影为点
轴上的射影为点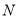 ,直线
,直线 交椭圆于另一点
交椭圆于另一点 .证明:对任意的
.证明:对任意的 ,点
,点 恒在以线段
恒在以线段 为直径的圆内.
为直径的圆内.
相关试题

