【题目】已知函数![]() (
(![]() 是自然对数的底数)
是自然对数的底数)
(1)若直线![]() 为曲线
为曲线![]() 的一条切线,求实数
的一条切线,求实数![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若
,若![]() 在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数
在定义域上有极值点(极值点是指函数取得极值时对应的自变量的值),求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:
(1)设切点,根据导数的几何意义求解.(2)分单调递增合递减两种情况考虑,将问题转化为导函数大(小)于等于零在![]() 恒成立求解可得
恒成立求解可得![]() 的范围.(3)由题意得
的范围.(3)由题意得![]() ,令
,令![]() ,然后对实数
,然后对实数![]() 的取值进行分类讨论,并根据
的取值进行分类讨论,并根据![]() 的符号去掉绝对值,再结合导数得到函数
的符号去掉绝对值,再结合导数得到函数![]() 的单调性,进而得到函数
的单调性,进而得到函数![]() 有极值时实数
有极值时实数![]() 的取值范围.
的取值范围.
试题解析:
(1)设切点![]() ,则
,则![]() (*)
(*)
又![]()
![]()
![]() ,代入(*)得
,代入(*)得![]()
![]()
![]() .
.
(2)设![]() ,
,
当![]() 单调递增时,
单调递增时,
则![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上恒成立,
上恒成立,
又![]()
![]() 解得
解得![]() .
.
当![]() 单调递减时,
单调递减时,
则![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上恒成立,
上恒成立,
![]()
![]()
综上![]() 单调时
单调时![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() ,
,
令![]() 则
则![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
∴![]() ,即
,即![]() .
.
1)当![]() ,即
,即![]() 时,
时, ![]()
∴![]() ,
,
则![]() 单调递增,
单调递增,
![]() 在
在![]() 上无极值点.
上无极值点.
2)当![]() 即
即![]() 时,
时, ![]()
![]()
∴![]()
I)当![]() ,即
,即![]() 时,
时, ![]()
![]() 在
在![]() 递增,
递增,
![]() ,
,
![]() 在
在![]() 上递增,
上递增,
![]() 在
在![]() 上无极值点.
上无极值点.
II)当![]() 时,由
时,由![]()
![]() 在
在![]() 递减,
递减, ![]() 递增,
递增,
又![]()
![]() 使得
使得![]()
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上有一个极小值点.
上有一个极小值点.
3)当![]() 时,
时, ![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]() ,
,
![]() 在
在![]() 上恒成立,
上恒成立,
![]() 无极值点.
无极值点.
4)当![]() 时,
时,
![]() 在
在![]() 递增,
递增,
![]() 使得
使得![]() ,
,
![]() 当
当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]() ,
,
 ,
,
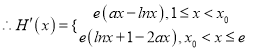 ,
,
令![]() ,
,
下面证明![]() ,即证
,即证![]() ,
,
又![]()
![]() ,
,
即证![]() ,所以结论成立,即
,所以结论成立,即![]() ,
,
![]() 在
在![]() 递减,
递减, ![]() 递增,
递增,
![]() 为
为![]() 的极小值.
的极小值.
综上当![]() 或
或![]() 时,
时, ![]() 在
在![]() 上有极值点.
上有极值点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的左、右焦点分别为
的左、右焦点分别为 和
和 ,离心率是
,离心率是 ,直线
,直线 过点
过点 交椭圆于
交椭圆于 ,
,  两点,当直线
两点,当直线 过点
过点 时,
时,  的周长为
的周长为 .
.(Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)当直线
 绕点
绕点 运动时,试求
运动时,试求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, 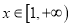 .
.(Ⅰ)讨论
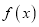 的单调性;
的单调性;(Ⅱ)若
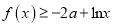 ,求实数
,求实数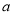 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某大型水上乐园内有一块矩形场地
 米,
米,  米,以
米,以 为直径的半圆
为直径的半圆 和半圆
和半圆 (半圆在矩形
(半圆在矩形 内部)为两个半圆形水上主题乐园,
内部)为两个半圆形水上主题乐园,  都建有围墙,游客只能从线段
都建有围墙,游客只能从线段 处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着
处进出该主题乐园.为了进一步提高经济效益,水上乐园管理部门决定沿着 修建不锈钢护栏,沿着线段
修建不锈钢护栏,沿着线段 修建该主题乐园大门并设置检票口,其中
修建该主题乐园大门并设置检票口,其中 分别为
分别为 上的动点,
上的动点,  ,且线段
,且线段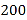 与线段
与线段 在圆心
在圆心 和
和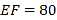 连线的同侧.已知弧线部分的修建费用为
连线的同侧.已知弧线部分的修建费用为 元/米,直线部门的平均修建费用为
元/米,直线部门的平均修建费用为 元/米.
元/米.
(1)若
 米,则检票等候区域(其中阴影部分)面积为多少平方米?
米,则检票等候区域(其中阴影部分)面积为多少平方米?(2)试确定点
 的位置,使得修建费用最低.
的位置,使得修建费用最低. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 的首项为
的首项为 ,前
,前 项和为
项和为 ,若对任意的
,若对任意的 ,均有
,均有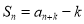 (
( 是常数且
是常数且 )成立,则称数列
)成立,则称数列 为“
为“ 数列”.
数列”.(1)若数列
 为“
为“ 数列”,求数列
数列”,求数列 的通项公式;
的通项公式;(2)是否存在数列
 既是“
既是“ 数列”,也是“
数列”,也是“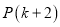 数列”?若存在,求出符合条件的数列
数列”?若存在,求出符合条件的数列 的通项公式及对应的
的通项公式及对应的 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)若数列
 为“
为“ 数列”,
数列”,  ,设
,设 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方体
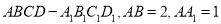 ,直线
,直线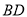 与平面
与平面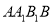 所成角为
所成角为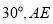 垂直
垂直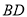 于点
于点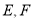 为
为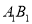 的中点.
的中点.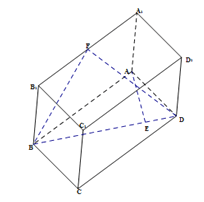
(1)求直线
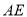 与平面
与平面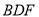 所成角的正弦值;
所成角的正弦值;(2)线段
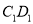 上是否存在点
上是否存在点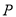 ,使得二面角
,使得二面角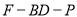 的余弦值为
的余弦值为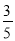 ?若存在,确定
?若存在,确定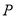 点位置;若不存在,说明理由.
点位置;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018江苏南京师大附中、天一、海门、淮阴四校高三联考】如图,一只蚂蚁从单位正方体
 的顶点
的顶点 出发,每一步(均为等可能性的)经过一条边到达另一顶点,设该蚂蚁经过
出发,每一步(均为等可能性的)经过一条边到达另一顶点,设该蚂蚁经过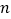 步回到点
步回到点 的概率
的概率 .
.
(I)分别写出
 的值;
的值;(II)设顶点
 出发经过
出发经过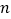 步到达点
步到达点 的概率为
的概率为 ,求
,求 的值;
的值;(III)求
 .
.
相关试题

