(本小题满分12分)

如图，已知三棱柱ABC—A1B1C1的侧棱与底面垂直，AA1＝AB＝AC＝1，AB⊥AC，M、N分别是CC1、BC的中点，点P在A1B1上，且满足＝λ(λ∈R).

(1)证明：PN⊥AM；

(2)当λ取何值时，直线PN与平面ABC所成的角θ最大？并求该最大角的正切值；

(3)若平面PMN与平面ABC所成的二面角为45°，试确定点P的位置.

解：(1)证明：如图，以AB，AC，AA1分别为x，y，z轴，建立空间直角坐标系A－xyz.

则P(λ，0,1)，N(，，0)，M(0,1，)，(2分)

从而＝(－λ，，－1)，＝(0,1，)，

·＝(－λ)×0＋×1－1×＝0，

所以PN⊥AM.(3分)

(2)平面ABC的一个法向量为n＝(0,0,1)，

则sinθ＝|sin(－〈，n〉)|＝|cos〈，n〉|

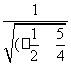＝||＝(※).(5分)

而θ∈[0，]，当θ最大时，sinθ最大，tanθ最大，θ＝除外，

由(※)式，当λ＝时，(sinθ)max＝，(tanθ)max＝2.(6分)

(3)平面ABC的一个法向量为n＝＝(0,0,1).

设平面PMN的一个法向量为m＝(x，y，z)，

由(1)得＝(λ，－1，).

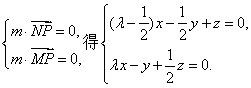由(7分)

解得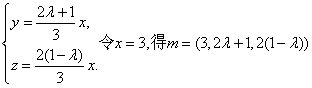. (9分)

∵平面PMN与平面ABC所成的二面角为45°，

∴|cos〈m，n〉|＝||＝＝，

解得λ＝－.(11分)

故点P在B1A1的延长线上，且|A1P|＝.(12分)

关闭