搜索
【题目】已知函数
，其中
．
（I）若
，求
在区间
上的最大值和最小值；
（II）解关于x的不等式
参考答案：
【答案】（1）最小值为
，最大值为
；（2）见解析
【解析】试题分析：（Ⅰ）a=1时，f（x）=（x﹣2）x=（x﹣1）2﹣1，由此能求出f（x）在区间[0，3]上的最大值和最小值，（Ⅱ）当a＞0时，原不等式同解于（x﹣2）（x﹣
）＞0，当a＜0时，原不等式同解于（x﹣2）（x﹣）＜0，由此能求出当a＞0时，不等式的解集为{x|x＞2或x＜}；当﹣1＜a＜0时，不等式的解集为{x|2＜x＜}；当a=﹣1时，不等式的解集为；当a＜﹣1时，不等式的解集为
．
详解：
(Ⅰ)最小值为
，最大值为
；
(Ⅱ)当
时，不等式解集为
当
时，不等式解集为
当
时，不等式解集为
当
时，不等式解集为
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆
经过
两点，且圆心在直线
上.（Ⅰ）求圆
的标准方程；（Ⅱ）设直线
经过点
，且与圆相交所得弦长为
，求直线的方程. -
科目： 来源： 题型：
查看答案和解析>>【题目】为评估一种农作物的种植效果，选了n块地作试验田．这n块地的亩产量（单位：
）分别为 
，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A. 的平均数
B. 的标准差
C. 的最大值
D. 的中位数 -
科目： 来源： 题型：
查看答案和解析>>【题目】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图.
根据该折线图，下列结论错误的是（ ）
A.月接待游客逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳 -
科目： 来源： 题型：
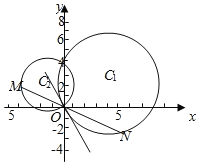
查看答案和解析>>【题目】已知圆
与y轴交于O，A两点，圆C2过O，A两点，且直线C2O与圆C1相切；（1）求圆C2的方程；
（2）若圆C2上一动点M，直线MO与圆C1的另一交点为N，在平面内是否存在定点P使得PM=PN始终成立，若存在求出定点坐标，若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某保险公司有一款保险产品的历史收益率（收益率=利润÷保费收入）的频率分布直方图如图所示：
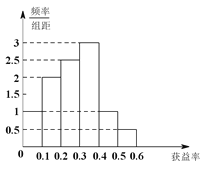
（Ⅰ）试估计平均收益率；
（Ⅱ）根据经验，若每份保单的保费在20元的基础上每增加
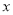元，对应的销量
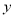（万份）与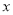
（元）有较强线性相关关系，从历史销售记录中抽样得到如下5组
与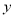
的对应数据：
据此计算出的回归方程为
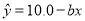.（i）求参数
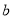的估计值；（ii）若把回归方程
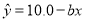当作
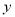与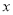
的线性关系，用（Ⅰ）中求出的平均收益率估计此产品的收益率，每份保单的保费定为多少元时此产品可获得最大收益，并求出该最大收益. -
科目： 来源： 题型：
查看答案和解析>>【题目】（本小题满分12分）一个盒子里装有三张卡片，分别标记有数字
，
，
，这三张卡片除标记的数字外完全相同。随机有放回地抽取次，每次抽取张，将抽取的卡片上的数字依次记为
，
，
.（Ⅰ）求“抽取的卡片上的数字满足
”的概率；（Ⅱ）求“抽取的卡片上的数字
，，不完全相同”的概率.
相关试题
