【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 是等边三角形,已知
是等边三角形,已知![]() ,
,![]() .
.
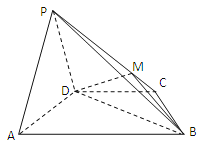
(1)设![]() 是
是![]() 上的一点,证明:平面
上的一点,证明:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)证得AD⊥BD,而面PAD⊥面ABCD,∴BD⊥面PAD,∴面MBD⊥面PAD.
(2)作辅助线PO⊥AD,则PO为四棱锥P—ABCD的高,求得S四边形ABCD=24.∴VP—ABCD=16![]() .
.
试题解析:
(1)证明:在△ABD中,∵AD=4,BD=8,AB=4![]() ,∴AD2+BD2=AB2.∴AD⊥BD.
,∴AD2+BD2=AB2.∴AD⊥BD.
又∵面PAD⊥面ABCD,面PAD∩面ABCD=AD,BD面ABCD,∴BD⊥面PAD.
又BD面BDM,∴面MBD⊥面PAD.
(2)解:过P作PO⊥AD,
∵面PAD⊥面ABCD,∴PO⊥面ABCD,即PO为四棱锥P—ABCD的高.
又△PAD是边长为4的等边三角形,∴PO=2![]() .
.
在底面四边形ABCD中,AB∥DC,AB=2DC,∴四边形ABCD为梯形.
在Rt△ADB中,斜边AB边上的高为![]() =
=![]() ,此即为梯形的高.
,此即为梯形的高.
∴S四边形ABCD=![]() ×
×![]() =24.
=24.
∴VP—ABCD=![]() ×24×2
×24×2![]() =16
=16![]() .
.
-
科目: 来源: 题型:
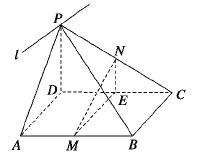
查看答案和解析>>【题目】如图,P为平行四边形ABCD所在平面外一点,MN分别为ABPC的中点,平面PAD∩平面PBC=l.
(1)判断BC与l的位置关系,并证明你的结论;
(2)判断MN与平面PAD的位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥
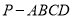 中,点
中,点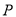 在平面
在平面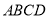 内的射影
内的射影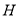 在棱
在棱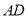 上,
上,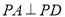 ,底面
,底面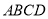 是梯形,
是梯形,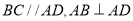 ,且
,且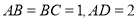 .
.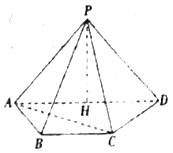
(1)求证:平面
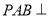 平面
平面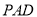 ;
;(2)若直线
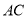 与
与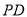 所成角为60°,求二面角
所成角为60°,求二面角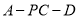 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1,F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为4的直角三角形.过B1作l交椭圆于P、Q两点,使PB2垂直QB2,求直线l的方程__________.
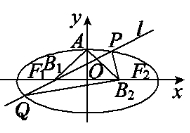
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
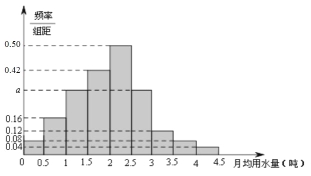
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥
 ,底面
,底面 为菱形,
为菱形,  平面
平面 ,
,  ,
,  分别是
分别是 的中点.
的中点.(Ⅰ)证明:
 ;
;(Ⅱ)若
 为
为 上的动点,
上的动点,  与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
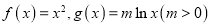 ,已知
,已知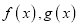 在
在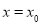 处的切线
处的切线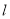 相同.
相同.(1)求
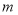 的值及切线
的值及切线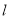 的方程;
的方程;(2)设函数
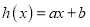 ,若存在实数
,若存在实数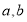 使得关于
使得关于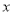 的不等式
的不等式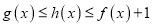 对
对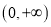 上的任意实数
上的任意实数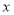 恒成立,求
恒成立,求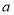 的最小值及对应的
的最小值及对应的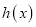 的解析式.
的解析式.
相关试题

