
【题目】设函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)若![]() 在
在![]() 上存在两个极值点,求
上存在两个极值点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,函数
,函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,且
,且![]() 线段的中点为
线段的中点为![]() ,证明:
,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
(Ⅰ)依题意![]() 在
在![]() 上存在两个极值点,等价于
上存在两个极值点,等价于![]() 在
在![]() 有两个不等实根,由
有两个不等实根,由![]() 参变分类可得
参变分类可得![]() ,令
,令![]() ,利用导数研究
,利用导数研究![]() 的单调性、极值,从而得到参数的取值范围;
的单调性、极值,从而得到参数的取值范围;
(Ⅱ)由题解得![]() ,
,![]() ,要证
,要证![]() 成立,只需证:
成立,只需证:![]() ,即:
,即:![]() ,只需证:
,只需证:![]() ,设
,设![]() ,即证:
,即证:![]() ,再分别证明
,再分别证明![]() ,
,![]() 即可;
即可;
解:(Ⅰ)由题意可知,![]() ,
,
![]() 在
在![]() 上存在两个极值点,等价于
上存在两个极值点,等价于![]() 在
在![]() 有两个不等实根,
有两个不等实根,
由![]() 可得,
可得,![]() ,令
,令![]() ,
,
则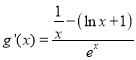 ,令
,令![]() ,
,
可得![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]()
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减;
单调递减;
所以![]() 是
是![]() 的极大值也是最大值,
的极大值也是最大值,![]() 又当
又当![]() ,当
,当![]() 大于0趋向与0,
大于0趋向与0,
要使![]() 在
在![]() 有两个根,则
有两个根,则![]() ,
,
所以![]() 的取值范围为
的取值范围为![]() ;
;
(Ⅱ)由题解得![]() ,
,![]() ,要证
,要证![]() 成立,
成立,
只需证:![]()
即:![]() ,
,
只需证:![]()
设![]() ,即证:
,即证:![]()
要证![]() ,只需证:
,只需证:![]()
令![]() ,则
,则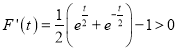
![]() 在
在![]() 上为增函数
上为增函数
![]() ,即
,即![]() 成立;
成立;
要证![]() ,只需证明:
,只需证明:![]()
令![]() ,则
,则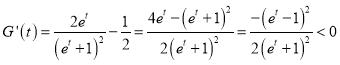
![]() 在
在![]() 上为减函数,
上为减函数,![]() ,即
,即![]() 成立
成立
![]() 成立,所以
成立,所以![]() 成立.
成立.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
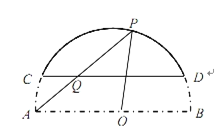
【题目】某房地产开发商在其开发的某小区前修建了一个弓形景观湖.如图,该弓形所在的圆是以![]() 为直径的圆,且
为直径的圆,且![]() 米,景观湖边界
米,景观湖边界![]() 与
与![]() 平行且它们间的距离为
平行且它们间的距离为![]() 米.开发商计划从
米.开发商计划从![]() 点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作
点出发建一座景观桥(假定建成的景观桥的桥面与地面和水面均平行),桥面在湖面上的部分记作![]() .设
.设![]() .
.
(1)用![]() 表示线段
表示线段![]() 并确定
并确定![]() 的范围;
的范围;
(2)为了使小区居民可以充分地欣赏湖景,所以要将![]() 的长度设计到最长,求
的长度设计到最长,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市春节大酬宾,购物满100元可参加一次抽奖活动,规则如下:顾客将一个半径适当的小球放入如图所示的容器正上方的人口处,小球在自由落下的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,顾客相应获得袋子里的奖品.已知小球每次遇到黑色障碍物时,向左向右下落的概率都为![]() .若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.
.若活动当天小明在该超市购物消费108元,按照活动规则,他可参加一次抽奖,则小明获得A袋中的奖品的概率为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问在
两点,试问在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?若存在,求出定点
恒成立?若存在,求出定点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com