

【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司![]() 年至
年至![]() 年的年利润
年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关).
的统计数据如下表(已知该公司的年利润与年份代号线性相关).
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 年(年份代号记为
年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由(Ⅰ)中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将(Ⅰ)中预测的该公司
级利润年.将(Ⅰ)中预测的该公司![]() 年的年利润视作该年利润的实际值,现从
年的年利润视作该年利润的实际值,现从![]() 年至
年至![]() 年这
年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式: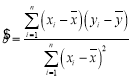 ,
,![]() .
.
【答案】(Ⅰ)![]() ,该公司
,该公司![]() 年年利润的预测值为
年年利润的预测值为![]() 亿元;(Ⅱ)
亿元;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求出![]() 和
和![]() 的值,将表格中的数据代入最小二乘法公式,求得
的值,将表格中的数据代入最小二乘法公式,求得![]() 和
和![]() 的值,进而可求得
的值,进而可求得![]() 关于
关于![]() 的线性回归方程,然后将
的线性回归方程,然后将![]() 代入回归直线方程,可得出该公司
代入回归直线方程,可得出该公司![]() 年年利润的估计值;
年年利润的估计值;
(Ⅱ)利用(Ⅰ)中的回归直线方程计算出从![]() 年至
年至![]() 年这
年这![]() 年被评为
年被评为![]() 级利润年的年数,然后利用组合计数原理结合古典概型的概率可得出所求事件的概率.
级利润年的年数,然后利用组合计数原理结合古典概型的概率可得出所求事件的概率.
(Ⅰ)根据表中数据,计算可得![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,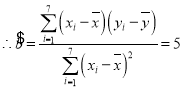 ,
,
![]() ,
,![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
将![]() 代入回归方程得
代入回归方程得![]() (亿元),
(亿元),
![]() 该公司
该公司![]() 年的年利润的预测值为
年的年利润的预测值为![]() 亿元.
亿元.
(Ⅱ)由(Ⅰ)可知![]() 年至
年至![]() 年的年利润的估计值分别为
年的年利润的估计值分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (单位:亿元),其中实际利润大于相应估计值的有
(单位:亿元),其中实际利润大于相应估计值的有![]() 年.
年.
故这![]() 年中被评为
年中被评为![]() 级利润年的有
级利润年的有![]() 年,评为
年,评为![]() 级利润年的有
级利润年的有![]() 年.
年.
记“从![]() 年至
年至![]() 年这
年这![]() 年的年利润中随机抽取
年的年利润中随机抽取![]() 年,恰有
年,恰有![]() 年为
年为![]() 级利润年”的概率为
级利润年”的概率为![]() ,
,![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,己知可引起感冒以及中东呼吸综合征(![]() )和严重急性呼吸综合征(
)和严重急性呼吸综合征(![]() )等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(
)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(![]() )是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.
某医院为筛查冠状病毒,需要检验血液是否为阳性,现有n(![]() )份血液样本,有以下两种检验方式:
)份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验n次.
方式二:混合检验,将其中k(![]() 且
且![]() )份血液样本分别取样混合在一起检验.
)份血液样本分别取样混合在一起检验.
若检验结果为阴性,这k份的血液全为阴性,因而这k份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份再逐份检验,此时这k份血液的检验次数总共为![]() .
.
假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为p(![]() ).现取其中k(
).现取其中k(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(1)若![]() ,试求p关于k的函数关系式
,试求p关于k的函数关系式![]() ;
;
(2)若p与干扰素计量![]() 相关,其中
相关,其中![]() (
(![]() )是不同的正实数,
)是不同的正实数,
满足![]() 且
且![]() (
(![]() )都有
)都有![]() 成立.
成立.
(i)求证:数列![]() 等比数列;
等比数列;
(ii)当![]() 时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
时,采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少,求k的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、点
、点![]() 及抛物线
及抛物线![]() .
.
(1)若直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,当
,当![]() 最大时求直线
最大时求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得过点
,使得过点![]() 的任一条直线与抛物线
的任一条直线与抛物线![]() 交于点
交于点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离相等?若存在,求出点
的距离相等?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)从样本中的运动达人中抽取7人参加“幸运抽奖”活动,通过抽奖共产生2位幸运用户,求这2位幸运用户恰好男用户和女用户各一位的概率.
附:
|
|
|
|
|
|
|
|
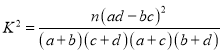
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成面积为
的两焦点与短轴的一个端点的连线构成面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆E的标准方程;
(2)直线![]() 与椭圆交于点A、B,线段
与椭圆交于点A、B,线段![]() 的中点为M,射线MO与椭圆交于点P,点O为
的中点为M,射线MO与椭圆交于点P,点O为![]() 的重心,试问:
的重心,试问:![]() 的面积S是否为定值,若是,求出这个值;若不是,求S的取值范围.
的面积S是否为定值,若是,求出这个值;若不是,求S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com