【题目】已知函数，函数，若，，使得不等式成立，则实数的取值范围为（ ）

A. B.

C. D.

【答案】D

【解析】

令t=，利用二次函数图像的性质求函数f（x）的最大值，令u=sinx∈[0,]对函数g（x）按a=0,a>0,a<0进行讨论求出函数最大值，由题可得f（x）max<g（x）max，解不等式即可得到所求范围．

，当时，令t=

可得,对称轴为，故最大值为，

即f(x)得最大值为，

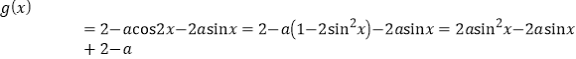
当时，令u=sinx∈[0,],则,

当a=0时，y=2,

当a<0时，二次函数对称轴为，故函数在对称轴处取到最大值为2-,

当a>0时，开口向上，0距对称轴远，故当u=0时取到最大值为2-a,

所以 ，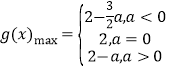

由题意可得f（x）max<g（x）max，

即当a<0时，，解得，故a<0,

当a=0时，，满足题意，

当a>0时，，解得，

综上可得，

故选：D．

关闭