【题目】如图甲,已知矩形![]() 中,
中, ![]() 为
为![]() 上一点,且
上一点,且![]() ,垂足为
,垂足为![]() ,现将矩形
,现将矩形![]() 沿对角线
沿对角线![]() 折起,得到如图乙所示的三棱锥
折起,得到如图乙所示的三棱锥![]() .
.

(Ⅰ)在图乙中,若![]() ,求
,求![]() 的长度;
的长度;
(Ⅱ)当二面角![]() 等于
等于![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)![]() (2)余弦值为
(2)余弦值为![]() .
.
【解析】试题分析:(Ⅰ)当![]() 时,由线面垂直的判定定理,可得
时,由线面垂直的判定定理,可得![]() 平面
平面![]() ,所以
,所以![]() ,由勾股定理求出BH的长度;(Ⅱ)以
,由勾股定理求出BH的长度;(Ⅱ)以![]() 为坐标原点,
为坐标原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,垂直于平面
轴,垂直于平面![]() 的方向为
的方向为![]() 轴建系,可得平面ADC的法向量为
轴建系,可得平面ADC的法向量为![]() ,由当二面角
,由当二面角![]() 等于
等于![]() ,求出点B,C,H三点的坐标,假设平面
,求出点B,C,H三点的坐标,假设平面![]() 的法向量
的法向量![]() ,由
,由![]() ,求出
,求出![]() ,根据两向量的夹角公式,求出二面角
,根据两向量的夹角公式,求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)由![]() ,可得折叠后
,可得折叠后![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
解得![]() ,
, ![]() ,由勾股定理,
,由勾股定理,
![]() .
.
(Ⅱ)如图,以![]() 为坐标原点,
为坐标原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,垂直于平面
轴,垂直于平面![]() 的方向为
的方向为![]() 轴建系,
轴建系,
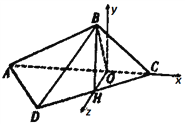
可得平面![]() 的法向量为
的法向量为![]() ,
,
即有![]() ,再由二面角
,再由二面角![]() 等于
等于![]() ,
,
可得![]() 点坐标为
点坐标为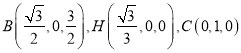 ,
,
所以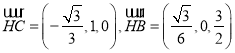 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则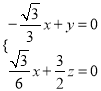
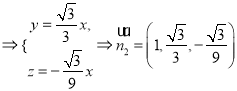 ,
,
所以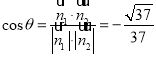 ,
,
由横坐标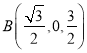 大于
大于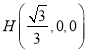 横坐标,
横坐标,
所以二面角![]() 为钝角,所以余弦值为
为钝角,所以余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=logax,g(x)=loga(2x+t﹣2)2 , (a>0,a≠1,t∈R).
(1)当t=4,x∈[1,2]时F(x)=g(x)﹣f(x)有最小值为2,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围.
(备注:函数y=x+ 在区间(0,1)上单调递减,在区间(1,+∞)上单调递增).
在区间(0,1)上单调递减,在区间(1,+∞)上单调递增). -
科目: 来源: 题型:
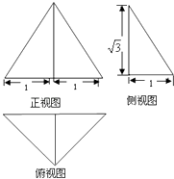
查看答案和解析>>【题目】一个简单几何体的三视图如图所示,其中正视图是一个正三角形,俯视图是等腰直角三角形,则该几何体的体积为 , 表面积为 .
-
科目: 来源: 题型:
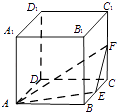
查看答案和解析>>【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|y=
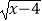 },B={x|﹣1≤2x﹣1≤0},则(RA)∩B=( )
},B={x|﹣1≤2x﹣1≤0},则(RA)∩B=( )
A.(4,+∞)
B.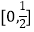
C.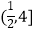
D.(1,4] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=ax2+x﹣a,a∈R
(1)若a=1,解不等式f(x)≥1;
(2)若a<0,解不等式f(x)>1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S﹣ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
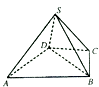
(Ⅰ)求证:SB=SD;
(Ⅱ)若∠BCD=120°,M为棱SA的中点,求证:DM∥平面SBC.
相关试题

