 如图,圆形花坛水池中央有一喷泉,水管OP=1m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2m,P距抛物线对称轴1m,则为使水不落到池外,水池直径最小为
如图,圆形花坛水池中央有一喷泉,水管OP=1m,水从喷头P喷出后呈抛物线状,先向上至最高点后落下,若最高点距水面2m,P距抛物线对称轴1m,则为使水不落到池外,水池直径最小为2+2
| 2 |
2+2
m.| 2 |
分析:建立直角坐标系,借助坐标法先求出落点的最远距离,从而计算出水池直径即可.
解答: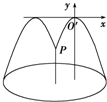 解:如图,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0),
解:如图,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0),
则P(-1,-1),代入抛物线方程得p=
,抛物线x2=-y,代点(x,-2),
得x=
,即水池半径最小为r=(1+
)m,
水池直径最小为2r=(2+2
)m.
故答案为:2+2
.
 解:如图,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0),
解:如图,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0),则P(-1,-1),代入抛物线方程得p=
| 1 |
| 2 |
得x=
| 2 |
| 2 |
水池直径最小为2r=(2+2
| 2 |
故答案为:2+2
| 2 |
点评:解决实际问题通常有几个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型,其中关键是建立数学模型.

