搜索
【题目】如图，四棱锥
中，底面
为梯形， 
， 
， 
，平面
平面
， 
.
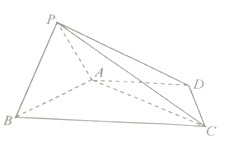
（1）求证： 
；
（2）是否存在点
，到四棱锥
各顶点的距离都相等？说明理由.
【答案】(1)见解析；（2）见解析.
【解析】试题分析：（1）
，平面
平面
，所以
平面
，得
；（2）点
是三个直角三角形
、
和
的共同斜边
的中点，所以
，所以存在点
（即点
）到四棱锥
各顶点的距离都相等.
试题解析：
（1）证明：设
的中点为
，连结
，在梯形
中，
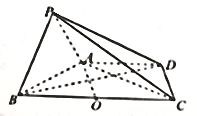
因为
， 
，
所以
为等边三角形，
又
所以四边形
为菱形， 
因为
， 
，所以
所以
， 
又平面
平面
， 
是交线， 
平面
所以
平面
又因为
平面
，所以
（2）解：因为
， 
， 
，所以
平面
所以
所以
为直角三角形， 
连结
，由（1）知
，
所以
所以
为直角三角形， 
.
所以点
是三个直角三角形
、
和
的共同斜边
的中点，
所以
，
所以存在点
（即点
）到四棱锥
各顶点的距离都相等.
