【题目】选修4—5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若存在实数![]() ,使得不等式
,使得不等式![]() 成立,求实
成立,求实![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据绝对值定义,将原不等式等价转化为三个不等式组,求它们的并集得原不等式的解集(2)不等式有解问题往往转化为对应函数最值问题:![]() ,由绝对值三角不等式得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,即转化为解不等式:
,由绝对值三角不等式得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,即转化为解不等式:![]() ,再利用绝对值定义求解得解集
,再利用绝对值定义求解得解集
试题解析:(1)当a=2时,f(x)=|x﹣3|﹣|x﹣2|,
当x≥3时,![]() ,即为
,即为![]() ,即
,即![]() 成立,则有x≥3;
成立,则有x≥3;
当x≤2时,![]() 即为
即为![]() ,即
,即![]() ,解得x∈;
,解得x∈;
当2<x<3时,![]() 即为
即为![]() ,解得,
,解得,![]() ,则有
,则有![]() .
.
则原不等式的解集为![]() 即为
即为![]() ;
;
(2)由绝对值不等式的性质可得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,
即有![]() 的最大值为|a﹣3|.
的最大值为|a﹣3|.
若存在实数x,使得不等式![]() 成立,则有
成立,则有![]()
即![]() 或
或![]() ,即有
,即有![]() ∈或
∈或![]() ≤
≤![]() .所以
.所以![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在
 上的函数
上的函数 对于任意实数
对于任意实数 ,都有
,都有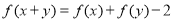 成立,且
成立,且 ,当
,当 时,
时, .
.(1)判断
 的单调性,并加以证明;
的单调性,并加以证明;(2)试问:当
 时,
时, 是否有最值?如果有,求出最值;如果没有,说明理由;
是否有最值?如果有,求出最值;如果没有,说明理由;(3)解关于
 的不等式
的不等式 ,其中
,其中 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】集合A={0,2,a},B={1,a2},若A∪B={0,1,2,4,16},则a的值为( )
A. 0 B. 1
C. 2 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了美化城市环境,某市针对市民乱扔垃圾现象进行罚款处理。为了更好的了解市民的态度,随机抽取了200人进行了调查,得到如下数据:
罚款金额
 (单位:元)
(单位:元)0
5
10
15
20
会继续乱扔垃圾的人数

80
50
40
20
10
(1)若乱扔垃圾的人数
 与罚款金额
与罚款金额 满足线性回归方程,求回归方程
满足线性回归方程,求回归方程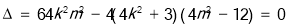 ,其中
,其中 ,并据此分析,要使乱扔垃圾者不超过
,并据此分析,要使乱扔垃圾者不超过 ,罚款金额至少是多少元?
,罚款金额至少是多少元?(2)若以调查数据为基础,从5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a3=1,公差d=2,则a8的值为( )
A. 9 B. 10 C. 11 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,射影定理可表示为a=b·cosC+c·cosB.其中a,b,c分别为角A,B,C的对边,类比上述定理.写出对空间四面体性质的猜想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比平面几何中的命题:“垂直于同一直线的两条直线平行”,在立体几何中,可以得到命题“__________”,这个类比命题的真假性是__________.
相关试题

