【题目】从某校高二年级学生中随机抽取了20名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.

![]() 求图中实数a的值;
求图中实数a的值;
![]() 若该校高二年级共有学生600名,试估计该校高二年级期中考试数学成绩不低于60分的人数;
若该校高二年级共有学生600名,试估计该校高二年级期中考试数学成绩不低于60分的人数;
![]() 若从数学成绩在[60,70)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值大于10的概率.
若从数学成绩在[60,70)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值大于10的概率.
参考答案:
【答案】(1)a=0.03.(2)510(3)![]()
【解析】试题分析:
本题主要考查用样本估计总体和随机抽样。
![]() 根据频率和为
根据频率和为![]() ,求出
,求出![]() 。
。
![]() 先求出成绩不低于
先求出成绩不低于![]() 分的频率,再乘以该校高二总人数。
分的频率,再乘以该校高二总人数。
![]() 先求出成绩在
先求出成绩在![]() ,分数段内的人数和成绩在
,分数段内的人数和成绩在![]() 分数段内的人数共
分数段内的人数共![]() 人,列出从这
人,列出从这![]() 名学生中随机选取两名学生的所有基本事件有
名学生中随机选取两名学生的所有基本事件有![]() 种,其中符合“这
种,其中符合“这![]() 名学生的数学成绩之差的绝对值不大于
名学生的数学成绩之差的绝对值不大于![]() ”的事件有
”的事件有![]() 种,所以求出概率为
种,所以求出概率为![]() 的值。
的值。
试题解析:
![]() 因为图中所有小矩形的面积之和等于1,
因为图中所有小矩形的面积之和等于1,
所以10×(0.005+0.01+0.02+a+0.025+0.01)=1, 解得a=0.03.
![]() 根据频率分布直方图,成绩不低于60分的频率为1-10×(0.005+0.01)=0.85.
根据频率分布直方图,成绩不低于60分的频率为1-10×(0.005+0.01)=0.85.
由于该校高二年级共有学生600名,利用样本估计总体的思想,可估计该校高二年级期中考试数学成绩不低于60分的人数约为600×0.85=510
![]() 成绩在[60,70)分数段内的人数为20×0.2=4,成绩在[90,100]分数段内的人数为20×0.1=2,则记在[60,70)分数段的四名同学为A1,A2,A3,A4,在[90,100]分数段内的两名同学为B1,B2.
成绩在[60,70)分数段内的人数为20×0.2=4,成绩在[90,100]分数段内的人数为20×0.1=2,则记在[60,70)分数段的四名同学为A1,A2,A3,A4,在[90,100]分数段内的两名同学为B1,B2.
若从这6名学生中随机抽取2人,则总的取法共有15种.
如果2名学生的数学成绩都在[60,70)分数段内或都在[90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定不大于10;如果一个成绩在[60,70)分数段内,另一个成绩在[90,100]分数段内,那么这2名学生的数学成绩之差的绝对值一定大于10.
则所取2名学生的数学成绩之差的绝对值大于10的取法有共8种取法![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 所求概率为P=
所求概率为P=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
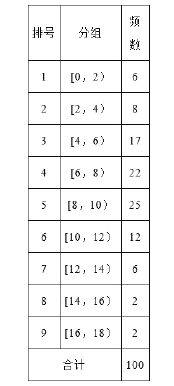
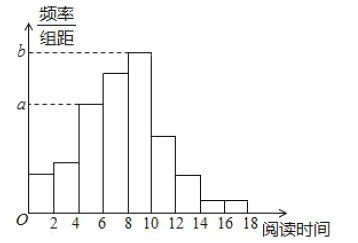
(Ⅰ)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(Ⅱ)求频率分布直方图中的
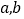 的值;
的值;(Ⅲ)从阅读时间在
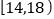 的学生中任选2人,求恰好有1人阅读时间在
的学生中任选2人,求恰好有1人阅读时间在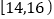 ,另1 人阅读时间在
,另1 人阅读时间在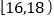 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班50位同学周考数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].

(1)求图中[80,90)的矩形高的值,并估计这50人周考数学的平均成绩;
(2)根据直方图求出这50人成绩的众数和中位数(精确到0.1);
(3)从成绩在[40,60)的学生中随机选取2人,求这2人成绩分别在[40,50)、[50,60)的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价
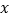 (元)
(元)18
19
20
21
22
销量
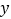 (册)
(册)61
56
50
48
45
(1)求试销5天的销量的方差和
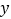 对
对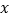 的回归直线方程;
的回归直线方程;(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,为了获得最大利润,该单元卷的单价卷的单价应定为多少元?
(附:
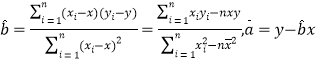 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 简单随机抽样每个个体被抽到的机会不一样,与先后有关
B. 由生物学知道生男生女的概率均为
 ,一对夫妇生两个孩子,则一定为一男一女
,一对夫妇生两个孩子,则一定为一男一女C. 互斥事件一定是对立事件,对立事件不一定是互斥事件
D. 老师在某班学号为1~50的50名学生中依次抽取学号为5,10,15,20,25,30,35,40,45,50的学生进行作业检查,这种抽样方法是系统抽样
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
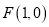 ,动点
,动点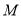 ,
, 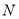 分别在
分别在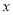 轴,
轴, 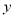 轴上运动,
轴上运动, 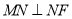 ,
, 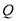 为平面上一点,
为平面上一点, 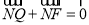 ,过点
,过点 作
作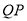 平行于
平行于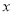 轴交
轴交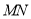 的延长线于点
的延长线于点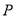 .
.(Ⅰ)求点
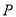 的轨迹曲线
的轨迹曲线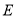 的方程;
的方程;(Ⅱ)过
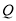 点作
点作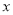 轴的垂线
轴的垂线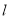 ,平行于
,平行于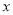 轴的两条直线
轴的两条直线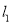 ,
, 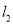 分别交曲线
分别交曲线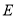 于
于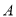 ,
, 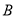 两点(直线
两点(直线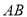 不过
不过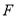 ),交
),交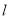 于
于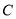 ,
, 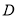 两点.若线段
两点.若线段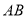 中点的轨迹方程为
中点的轨迹方程为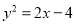 ,求
,求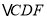 与
与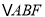 的面积之比.
的面积之比.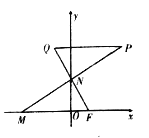
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:函数f(x)=Asin(ωx+)(A>0,ω>0,||<
 )的部分图象如图所示:
)的部分图象如图所示: 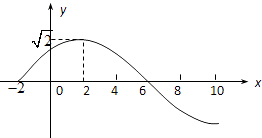
(1)求函数f(x)的解析式;
(2)若g(x)的图象是将f(x)的图象先向右平移1个单位,然后纵坐标不变横坐标缩短到原来的一半得到的,求g(x)的单调递增区间.
相关试题

