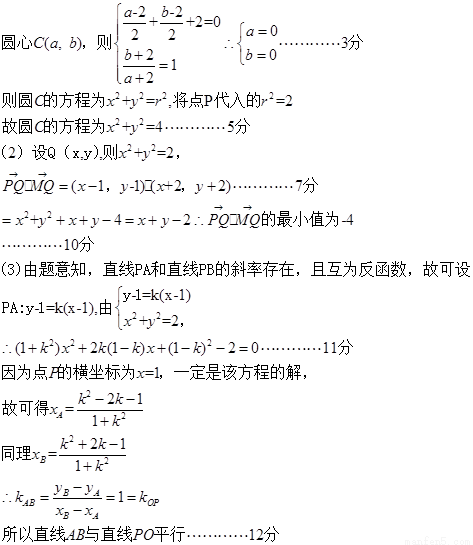已知圆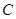 过点
过点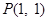 ,且与圆
,且与圆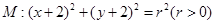 关于直线
关于直线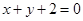 对称.
对称.
(1)求圆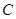 的方程;
的方程;
(2)设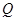 为圆
为圆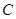 上一个动点,求
上一个动点,求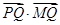 的最小值;
的最小值;
(3)过点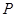 作两条相异直线分别与圆
作两条相异直线分别与圆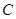 相交于
相交于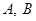 ,且直线
,且直线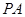 和
和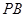 直线的倾斜角互补,
直线的倾斜角互补,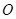 为坐标原点,试判断直线
为坐标原点,试判断直线 和
和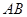 是否平行,并说明理由.
是否平行,并说明理由.
【答案】
见解析.
【解析】第一问中,利用设圆心坐标,然后利用圆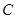 过点
过点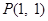 ,且与圆
,且与圆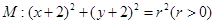 关于直线
关于直线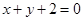 对称.
对称.
则可得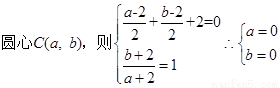
得到圆的方程。
第二问中,
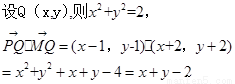 利用坐标法求解。
利用坐标法求解。
第三问中,设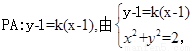 得到关于A点的横坐标,同理可得B的横坐标,然后借助于直线方程,和斜率公式求解得到。
得到关于A点的横坐标,同理可得B的横坐标,然后借助于直线方程,和斜率公式求解得到。
解:设