【题目】已知点F(0,1),直线l:y=﹣1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1 , |DB|=l2 , 求 ![]() 的最大值.
的最大值.
参考答案:
【答案】
(1)解:设P(x,y),则Q(x,﹣1),
∵ ![]() ,
,
∴(0,y+1)(﹣x,2)=(x,y﹣1)(x,﹣2).
即2(y+1)=x2﹣2(y﹣1),即x2=4y,
所以动点P的轨迹C的方程x2=4y
(2)解:设圆M的圆心坐标为M(a,b),则a2=4b.①
圆M的半径为 ![]() .
.
圆M的方程为(x﹣a)2+(y﹣b)2=a2+(b﹣2)2.
令y=0,则(x﹣a)2+b2=a2+(b﹣2)2,
整理得,x2﹣2ax+4b﹣4=0.②
由①、②解得,x=a±2.
不妨设A(a﹣2,0),B(a+2,0),
∴ ![]() ,
, ![]() .
.
∴ ![]() =
=  ,③
,③
当a≠0时,由③得, 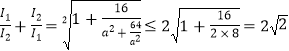 .
.
当且仅当 ![]() 时,等号成立.
时,等号成立.
当a=0时,由③得, ![]() =2.
=2.
故当 ![]() 时,
时, ![]() 的最大值为
的最大值为 ![]() .
.
【解析】(1)先设出点P的坐标,代入 ![]() 整理即可得到动点P的轨迹C的方程;(2)先利用条件设出圆的方程,并求出A、B两点的坐标以及|DA|=l1 , |DB|=l2的表达式,代入
整理即可得到动点P的轨迹C的方程;(2)先利用条件设出圆的方程,并求出A、B两点的坐标以及|DA|=l1 , |DB|=l2的表达式,代入 ![]() 整理后利用基本不等式求最大值即可.
整理后利用基本不等式求最大值即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
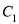 的极坐标方程为
的极坐标方程为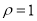 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为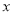 的正半轴,建立平面直角坐标系
的正半轴,建立平面直角坐标系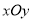 .
.(1)若曲线
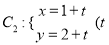 为参数)与曲线
为参数)与曲线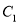 相交于两点
相交于两点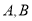 ,求
,求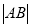 ;
;(2)若
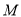 是曲线
是曲线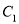 上的动点,且点
上的动点,且点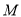 的直角坐标为
的直角坐标为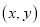 ,求
,求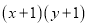 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
t
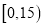
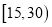
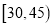
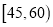
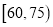
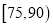
男同学人数
7
11
15
12
2
1
女同学人数
8
9
17
13
3
2
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为
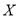 ,求
,求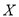 的分布列和数学期望
的分布列和数学期望 -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足
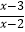 ≤0,
≤0,
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|3≤x<6},B={y|y=2x , 2≤x<3},U=R.
(1)求A∪B;
(2)求(UA)∩B. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=|x+1|+|x﹣1|.
(1)求f(x)≤x+2的解集;
(2)若不等式f(x)≤log2(a2﹣4a+12)对任意实数a恒成立,求x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣a(1﹣
 ).
).
(1)若a=1,求f(x)的单调区间;
(2)若f(x)≥0,对任意的x≥1均成立,求实数a的取值范围;
(3)求证:( )1008>
)1008>  .
.
相关试题

