搜索
【题目】2006 年 8 月中旬 , 湖南省资兴市遇到了百年不遇的洪水灾害 . 在资兴市的东江湖岸边的点 O 处(可视湖岸为直线) 停放着一只救人的小船，由于缆绳突然断开，小船被风刮跑，其方向与湖岸成 15°，, 速度为2.5 km/ h ，同时，岸上有一人从同一地点开始追赶小船 .已知他在岸上追的速度为4 km/ h ，在水中游的速度为 2 km/h .问此人能否追上小船? 若小船速度改变 ，则小船能被此人追上的最大速度是多少 ?
参考答案：
【答案】答案见解析.
【解析】
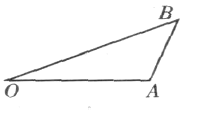
如图所示，设此人在岸上跑到点
后下水, 在点
处追上小船.设船速为
,人追上船的时间为
, 人在岸上追船的时间为的
倍(
), 则人在水中游的时间为
.
故
，
.
由余弦定理得
.
整理得
.
设
.
易知
.
（1）若
，则必存在
，使得
.
此时，
，解得
.
（2）若
，要使
在
内有解，
则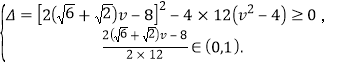
解得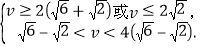
故
.
综上，当
时，人可以追上船.
因此，船速为25km/h时，能追上小船，小船能被人追上的最大速度是
km/h.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
，
.（1）若曲线
与
在点
处有相同的切线，求函数
的极值；（2）若
，讨论函数
的单调性. -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）6个人按下列要求站一横排，甲、乙必须相邻，有多少种不同的站法？
（2）6个人按下列要求站一横排，甲不站左端，乙不站右端．有多少种不同的站法？
（3）用0，1，2，3，4，5这六个数字可以组成多少个六位数且是奇数（无重复数字的数）？
（4）用0，1，2，3，4，5这六个数字可以组成多少个个位上的数字不是5的六位数（无重复数字的数）？
-
科目： 来源： 题型：
查看答案和解析>>【题目】“一本书，一碗面，一条河，一座桥”曾是兰州的城市名片，而现在“兰州马拉松”又成为了兰州的另一张名片，随着全民运动健康意识的提高，马拉松运动不仅在兰州，而且在全国各大城市逐渐兴起，参与马拉松训练与比赛的人口逐年增加．为此，某市对人们参加马拉松运动的情况进行了统计调查．其中一项调查是调查人员从参与马拉松运动的人中随机抽取200人，对其每周参与马拉松长跑训练的天数进行统计，得到以下统计表：
平均每周进行长跑训练天数
不大于2天
3天或4天
不少于5天
人数
30
130
40
若某人平均每周进行长跑训练天数不少于5天，则称其为“热烈参与者”，否则称为“非热烈参与者”．
（1）经调查，该市约有2万人参与马拉松运动，试估计其中“热烈参与者”的人数；
（2）根据上表的数据，填写下列2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“热烈参与马拉松”与性别有关？
热烈参与者
非热烈参与者
合计
男
140
女
55
合计
附：k2=
（n为样本容量）P（k2≥k0）
0.500
0.400
0.250
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k0
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目： 来源： 题型：
查看答案和解析>>【题目】某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（第
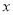周）和市场占有率（
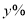）的几组相关数据如下表：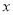
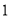
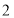
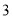
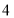
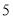
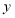
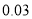
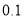
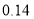
（1）根据表中的数据，用最小二乘法求出
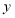关于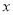的线性回归方程
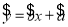；（2）根据上述线性回归方程，预测在第几周，该款旗舰机型市场占有率将首次超过
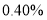（最后结果精确到整数）．参考公式：
，
． -
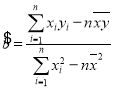科目： 来源： 题型：
查看答案和解析>>【题目】已知奇函数f（x）
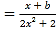，函数g（θ）＝cos2θ+2sinθ
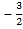，θ∈[m，
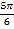]．m，b∈R．（1）求b的值；
（2）判断函数f（x）在[0，1]上的单调性，并证明；
（3）当x∈[0，1]时，函数g（θ）的最小值恰为f（x）的最大值，求m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】回答下列两个问题, 并给出例子或证明.
(1)对任意正整数
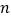, 在平面上是否都存在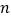个不在同一条直线上的点, 使得任意两点间的距离都为正整数?(2)在平面上是否存在两两不同的无限点列组成的点集
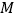, 使得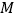内所有点不在同一条直线上, 且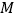内任意两点间的距离为正整数?
相关试题
