
【题目】如图在三棱柱![]() 中,
中,![]() 为
为![]() 边的中点,
边的中点,![]() .
.
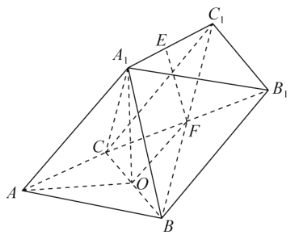
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 为
为![]() 中点且
中点且![]() ,
,![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用三角形中位线的性质得出![]() ,利用线面平行的判定定理可证得
,利用线面平行的判定定理可证得![]() 平面
平面![]() ;
;
(2)证明出![]() 平面
平面![]() ,由此可得出
,由此可得出![]() 、
、![]() 、
、![]() 两两垂直,然后以点
两两垂直,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴的正方向建立空间直角坐标系,利用空间向量法可求得平面
轴的正方向建立空间直角坐标系,利用空间向量法可求得平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
(1)在三棱柱![]() 中,侧面
中,侧面![]() 为平行四边形,
为平行四边形,
由![]() ,可知
,可知![]() 为
为![]() 的中点,又因为
的中点,又因为![]() 为
为![]() 边的中点,所以
边的中点,所以![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
取![]() 中点
中点![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() ,
,
又![]() ,所以满足
,所以满足![]() ,
,![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 、
、![]() 、
、![]() 两两相互垂直,
两两相互垂直,
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴的正方向建立空间直角坐标系(如图示),
轴的正方向建立空间直角坐标系(如图示),
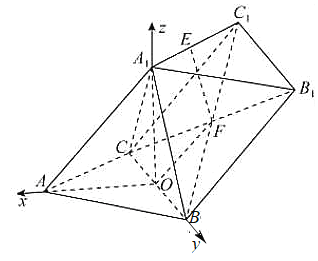
所以![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则有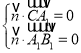 ,即
,即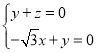 ,取
,取![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量可以取为
的法向量可以取为![]() ,
,
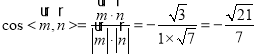 ,
,
所以平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】百年大计,教育为本.某校积极响应教育部号召,不断加大拔尖人才的培养力度,为清华、北大等排名前十的名校输送更多的人才.该校成立特长班进行专项培训.据统计有如下表格.(其中![]() 表示通过自主招生获得降分资格的学生人数,
表示通过自主招生获得降分资格的学生人数,![]() 表示被清华、北大等名校录取的学生人数)
表示被清华、北大等名校录取的学生人数)
年份(届) | 2014 | 2015 | 2016 | 2017 | 2018 |
| 41 | 49 | 55 | 57 | 63 |
| 82 | 96 | 108 | 106 | 123 |
(1)通过画散点图发现![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(保留两位有效数字)
的线性回归方程;(保留两位有效数字)
(2)若已知该校2019年通过自主招生获得降分资格的学生人数为61人,预测2019年高考该校考人名校的人数;
(3)若从2014年和2018年考人名校的学生中采用分层抽样的方式抽取出5个人回校宣传,在选取的5个人中再选取2人进行演讲,求进行演讲的两人是2018年毕业的人数![]() 的分布列和期望.
的分布列和期望.
参考公式: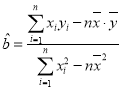 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的图象经过点
的图象经过点![]() .
.
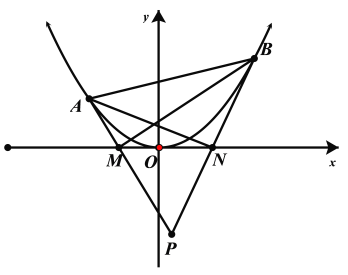
(1)求抛物线![]() 的方程和焦点坐标;
的方程和焦点坐标;
(2)直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 不同两点,且
不同两点,且![]() ,
,![]() 位于
位于![]() 轴两侧,过点
轴两侧,过点![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的两条切线交于点
的两条切线交于点![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴的交点分别记作
轴的交点分别记作![]() ,
,![]() .记
.记![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,
,![]() 面积为
面积为![]() ,试问
,试问![]() 是否为定值,若是,请求出该定值;若不是,请说明理由.
是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日,是中华人民共和国成立70周年纪念日.70年砥砺奋进,70年波澜壮阔,感染、激励着一代又一代华夏儿女,为祖国的繁荣昌盛努力拼搏,奋发图强.为进一步对学生进行爱国教育,某校社会实践活动小组,在老师的指导下,从学校随机抽取四个班级160名同学对这次国庆阅兵受到激励情况进行调查研究,记录的情况如下图:

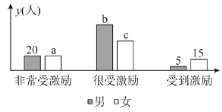
(1)如果从这160人中随机选取1人,此人非常受激励的概率和此人是很受激励的女同学的概率都是![]() ,求
,求![]() 的值;
的值;
(2)根据“非常受激励”与“很受激励”两种情况进行研究,判断是否有![]() 的把握认为受激励程度与性别有关.
的把握认为受激励程度与性别有关.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络商城在![]() 年
年![]() 月
月![]() 日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了
日开展“庆元旦”活动,当天各店铺销售额破十亿,为了提高各店铺销售的积极性,采用摇号抽奖的方式,抽取了![]() 家店铺进行红包奖励.如图是抽取的
家店铺进行红包奖励.如图是抽取的![]() 家店铺元旦当天的销售额(单位:千元)的频率分布直方图.
家店铺元旦当天的销售额(单位:千元)的频率分布直方图.
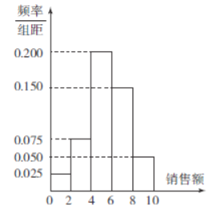
(1)求抽取的这![]() 家店铺,元旦当天销售额的平均值;
家店铺,元旦当天销售额的平均值;
(2)估计抽取的![]() 家店铺中元旦当天销售额不低于
家店铺中元旦当天销售额不低于![]() 元的有多少家;
元的有多少家;
(3)为了了解抽取的各店铺的销售方案,销售额在![]() 和
和![]() 的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在
的店铺中共抽取两家店铺进行销售研究,求抽取的店铺销售额在![]() 和
和![]() 各一个的概率.
各一个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体ABCDPE中,四边形ABCD是直角梯形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的余弦值为
的余弦值为![]() ,
,![]() ,F为BE中点,G为PD中点.
,F为BE中点,G为PD中点.
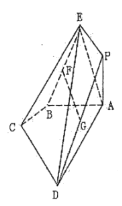
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)求平面BCE与平面ADE所成角(锐角)的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com