【题目】我国于2015年10月宣布实施普遍二孩政策，为了解户籍、性别对生育二胎选择倾向的影响，某地从育龄群体中随机抽取了容量为140的调查样本，其中城镇户籍与农村户籍各70人；男性60人，女性80人，绘制的不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图如图所示，其中阴影部分表示倾向选择生育二胎的对应比例，则下列叙述正确的是（ ）
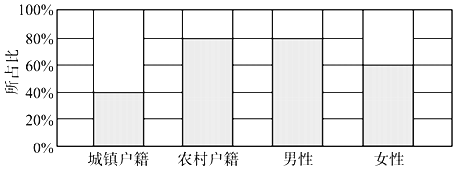
A.是否倾向选择生育二胎与户籍有关
B.是否倾向选择生育二胎与性别有关
C.调查样本中倾向选择生育二胎的群群中，男性人数与女性人数相同
D.倾向选择不生育二胎的群群中，农村户籍人数多于城镇户籍人数
【答案】ABCD
【解析】
由比例图，可得是否倾向选择生育二胎与户籍、性别有关，倾向选择不生育二胎的人员中，农村户籍人数少于城镇户籍人数，倾向选择生育二胎的人员中的男性人数与女性人数，即可得出结论.
由不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图，知：
在A中，城镇户籍倾向选择生育二胎的比例为
，农村户籍倾向选择生育二胎的比例为
，
∴是否倾向选择生育二胎与户籍有关，故A正确；
在B中，男性倾向选择生育二胎的比例为，女性倾向选择生育二胎的比例为
，
∴是否倾向选择生育二胎与性别有关，故B正确；
在C中，男性倾向选择生育二胎的比例为，人数为
人，
女性倾向选择生育二胎的比例为，人数为
人，
∴倾向选择生育二胎的人员中，男性人数与女性人数相同，故C正确；
在D中，倾向选择不生育二胎的人员中，农村户籍人数为
人，
城镇户籍人数为
人，
∴倾向选择不生育二胎的人员中，农村户籍人数少于城镇户籍人数，故D正确.
故选：ABCD.
天天向上口算本系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，以O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ2（cos2θ+3sin2θ）＝12，直线l的参数方程为
（t为参数），直线l与曲线C交于M，N两点.
（1）若点P的极坐标为（2，π），求|PM||PN|的值；
（2）求曲线C的内接矩形周长的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，右焦点为
，以原点
为圆心，椭圆
的短半轴长为半径的圆与直线
相切.
（1）求椭圆的方程；
（2）如图，过定点
的直线
交椭圆于
两点，连接
并延长交于
，求证：
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】调味品品评师的重要工作是对各种品牌的调味品进行品尝，分析、鉴定，调配、研发，周而复始、反复对比.对调味品品评师考核测试的一种常用方法如下：拿出n瓶外观相同但品质不同的调味品让其品尝，要求其按品质优劣为它们排序；经过一段时间，等其记忆淡忘之后，再让其品尝这n瓶调味品，并重新按品质优劣为它们排序，这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分.现设
，分别以
，
，
，
表示第一次排序时被排为1，2，3，4的四种调味品在第二次排序时的序号，并令
，则X是对两次排序的偏离程度的一种描述.（如第二次排序时的序号为1，3，2，4，则
）.
（1）写出X的所有可能值构成的集合；
（2）假设，，
的排列等可能地为1，2，3，4的各种排列，求X的数学期望；
（3）某调味品品评师在相继进行的三轮测试中，都有
.
（i）试按（2）中的结果，计算出现这种现象的概率（假定各轮测试相互独立）；
（ⅱ）请你判断该调味品品评师的品味鉴别能力如何？并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】11月，2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办，其间甲、乙两人轮流进行篮球定点投篮比赛（每人各投一次为一轮），在相同的条件下，每轮甲乙两人在同一位置，甲先投，每人投一次球，两人有1人命中，命中者得1分，未命中者得-1分；两人都命中或都未命中，两人均得0分，设甲每次投球命中的概率为
，乙每次投球命中的概率为
，且各次投球互不影响.
（1）经过1轮投球，记甲的得分为
，求的分布列；
（2）若经过
轮投球，用
表示经过第
轮投球，累计得分，甲的得分高于乙的得分的概率.
①求
；
②规定
，经过计算机计算可估计得
，请根据①中的值分别写出a，c关于b的表达式，并由此求出数列
的通项公式.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】微信是腾讯公司推出的一种手机通讯软件，它支持发送语音、短信、视频、图片和文字，一经推出便风靡全国，甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间，某经销化妆品的微商在一广场随机采访140位市民进行调查，其中每天玩微信超过6小时的用户称为“微信控”，否则称其为“非微信控”， 调查结果统计如下:
微信控 | 非微信控 | 合计 | |
女性 | 60 | ||
男性 | 30 | ||
合计 | 70 | 140 |
（1）根据以上数据，把表格中的数据填写完整；
（2）利用（1）完成的表格数据回答下列问题：
①是否在犯错误的概率不超过0.001的前提下认为“微信控”与“性别”有关；
②已知在被调查的女性“微信控”市民中有5位退休老人，其中2位是教师，现从这5位退休老人中随机抽取2人，求至少有1位老师的概率.
附表：
其中
P(K2≥k) | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
