[题目]某人某天的工作是驾车从地出发.到两地办事.最后返回地.,三地之间各路段行驶时间及拥堵概率如下表路段正常行驶所用时间上午拥堵概率下午拥堵概率10．30．620．20．730．30．9若在某路段遇到拥堵.则在该路段行驶时间需要延长1小时．现有如下两个方案:方案甲:上午从地出发到地办事然后到达地.下午从地办事后返回地,方案乙:上午从地� 题目和参考答案——青夏教育精英家教网—

【题目】某人某天的工作是驾车从地出发，到两地办事，最后返回地，,三地之间各路段行驶时间及拥堵概率如下表

路段	正常行驶所用时间（小时）	上午拥堵概率	下午拥堵概率
	1	0．3	0．6
	2	0．2	0．7
	3	0．3	0．9

若在某路段遇到拥堵，则在该路段行驶时间需要延长1小时．

现有如下两个方案：

方案甲：上午从地出发到地办事然后到达地，下午从地办事后返回地；

方案乙：上午从地出发到地办事，下午从地出发到达地，办完事后返回地．

（1）若此人早上8点从地出发，在各地办事及午餐的累积时间为2小时，且采用方案甲，求他当日18点或18点之前能返回地的概率．

（2）甲乙两个方案中，哪个方案有利于办完事后更早返回地？请说明理由.

【答案】（1）；（2）采用甲方案能更早返回，理由见解析.

【解析】

（1）由题意可知能按时返回的充要条件是拥堵路段不超过两段，则不能按时，返回时由三段拥堵，二者互为对立事件，利用对立事件的概率公式，即可求解.

（2）设某段路正常行驶时间为，拥堵的概率为，可得该路段行驶时间的分布列，利用公式求得期望.

（1）由题可知能按时返回的充要条件是拥堵路段不超过两段，则不能按时返回时有三段路段拥堵，二者互为对立事件，记“不能按时返回为事件”则，

所以能够按时返回的概率，

（2）设某段路正常行驶时间为,拥堵的概率为，

则该路段行驶时间的分布列为

行驶时间
概率

故，

上午路段行驶时间期望值分别为1．3小时2．2小时、3．3小时，

下午路段行驶时间期望值分别为1．6小时2．7小时3．9小时，

设采用甲方案所花费总行驶时间为,则小时，

设采用乙方案所花费总行驶时间为Z,则EZ=3．3+2．7+1．6=7．6小时，

因此采用甲方案能更早返回.

练习册系列答案

中考第三轮复习冲刺专用模拟试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某市政府为减轻汽车尾气对大气的污染，保卫蓝天，鼓励广大市民使用电动交通工具出行，决定为电动车（含电动自行车和电动汽车）免费提供电池检测服务.现从全市已挂牌照的电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测，电池性能分为需要更换、尚能使用、较好、良好四个等级，并分成电动自行车和电动汽车两个群体分别进行统计，样本分布如图.

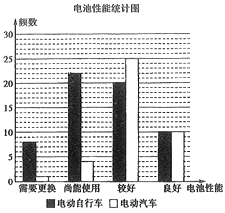
（1）采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆，再从这9辆中随机抽取2辆，求至少有一辆为电动汽车的概率；

（2）为进一步提高市民对电动车的使用热情，市政府准备为电动车车主一次性发放补助，标准如下：①电动自行车每辆补助300元；②电动汽车每辆补助500元；③对电池需要更换的电动车每辆额外补助400元.试求抽取的100辆电动车执行此方案的预算；并利用样本估计总体，试估计市政府执行此方案的预算.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，多面体是正三棱柱（底面是正三角形的直棱柱）沿平面切除一部分所得，其中平面为原正三棱柱的底面，，点D为的中点.

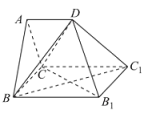
(1)求证：平面；

(2)求二面角的平面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆的离心率为，且过点．

（1）求的方程；

（2）是否存在直线与相交于两点，且满足：①与（为坐标原点）的斜率之和为2；②直线与圆相切，若存在，求出的方程；若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥平面ABCD，，E为PD的中点，F在AD上且．

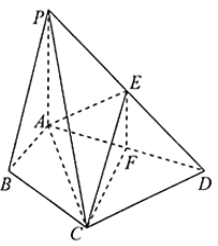
（1）求证：CE//平面PAB；

（2）若PA=2AB=2，求四面体PACE的体积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率，选取名工人，将他们随机分成两组，每组人.第一组工人用第一种生产方式，第二组工人用第二种生产方式.根据工人完成生产任务的工作时间（单位：）绘制了如图所示的茎叶图（茎为十位数，叶为个位数）：

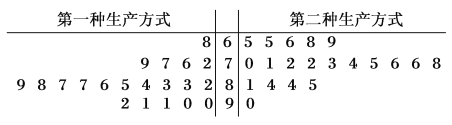
（1）根据茎叶图，估计两种生产方式完成任务所需时间至少分钟的概率，并对比两种生产方式所求概率，判断哪种生产方式的效率更高？

（2）将完成生产任务所需时间超过和不超过的工人数填入下面的列联表：

	超过	不超过
第一种生产方式
第二种生产方式

（3）根据（2）中的列联表，能否有的把握认为两种生产方式的效率有差异？

附：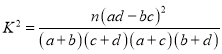

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】冠状病毒是一个大型病毒家族，己知可引起感冒以及中东呼吸综合征（）和严重急性呼吸综合征（）等较严重疾病.而今年出现在湖北武汉的新型冠状病毒（）是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中，感染可导致肺炎、严重急性呼吸综合征、肾衰竭，甚至死亡.

某医院为筛查冠状病毒，需要检验血液是否为阳性，现有n（）份血液样本，有以下两种检验方式：

方式一：逐份检验，则需要检验n次.

方式二：混合检验，将其中k（且）份血液样本分别取样混合在一起检验.

若检验结果为阴性，这k份的血液全为阴性，因而这k份血液样本只要检验一次就够了，如果检验结果为阳性，为了明确这k份血液究竟哪几份为阳性，就要对这k份再逐份检验，此时这k份血液的检验次数总共为.

假设在接受检验的血液样本中，每份样本的检验结果是阳性还是阴性都是独立的，且每份样本是阳性结果的概率为p（）.现取其中k（且）份血液样本，记采用逐份检验方式，样本需要检验的总次数为，采用混合检验方式，样本需要检验的总次数为.

（1）若，试求p关于k的函数关系式；

（2）若p与干扰素计量相关，其中（）是不同的正实数，

满足且（）都有成立.

（i）求证：数列等比数列；

（ii）当时，采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数的期望值更少，求k的最大值

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】埃及金字塔是古埃及的帝王（法老）陵墓，世界七大奇迹之一，其中较为著名的是胡夫金字塔．令人吃惊的并不仅仅是胡夫金字塔的雄壮身姿，还有发生在胡夫金字塔上的数字“巧合”．如胡夫金字塔的底部周长如果除以其高度的两倍，得到的商为3.14159，这就是圆周率较为精确的近似值．金字塔底部形为正方形，整个塔形为正四棱锥，经古代能工巧匠建设完成后，底座边长大约230米．因年久风化，顶端剥落10米，则胡夫金字塔现高大约为（）

A.128.5米B.132.5米C.136.5米D.110.5米

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数，函数与直线相切，其中，，是自然对数的底数．