
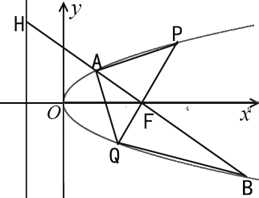
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,将该直线方程与抛物线的方程联立,消去
,将该直线方程与抛物线的方程联立,消去![]() ,得到关于
,得到关于![]() 的二次方程,利用韦达定理结合
的二次方程,利用韦达定理结合![]() 可求出正数
可求出正数![]() 的值;
的值;
(2)由直线![]() 与坐标轴不垂直,所以设
与坐标轴不垂直,所以设![]() 方程为
方程为![]() ,并设点
,并设点![]() ,将直线
,将直线![]() 的方程与抛物线的方程联立,列出韦达定理,并求出
的方程与抛物线的方程联立,列出韦达定理,并求出![]() ,求出点
,求出点![]() 的坐标,可得出点
的坐标,可得出点![]() 的坐标,并可得出直线
的坐标,并可得出直线![]() 的方程,将该直线方程与抛物线的方程联立,利用韦达定理得出点
的方程,将该直线方程与抛物线的方程联立,利用韦达定理得出点![]() 的坐标,并分别计算出点
的坐标,并分别计算出点![]() 、
、![]() 到直线
到直线![]() 的距离
的距离![]() 、
、![]() ,利用三角形的面积公式可得出
,利用三角形的面积公式可得出![]() 关于
关于![]() 的表达式,设
的表达式,设![]() ,构造函数
,构造函数![]() ,利用导数求出函数
,利用导数求出函数![]() 的最小值,即可得出
的最小值,即可得出![]() 的最小值.
的最小值.
(1)设![]() 方程为
方程为![]() ,与
,与![]() 联立,消去
联立,消去![]() 整理得
整理得![]() ,
,
所以![]() ,得
,得![]() (舍去)或
(舍去)或![]() ;
;
(2)由(1)知抛物线方程为![]() ,
,![]() ,准线方程为
,准线方程为![]() .
.
因为直线![]() 与坐标轴不垂直,所以设
与坐标轴不垂直,所以设![]() 方程为
方程为![]() ,
,![]() ,
,
由![]() 得
得![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,由
,由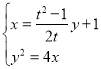 得
得![]() ,
,
所以![]() ,
,![]() ,代入
,代入![]() ,得
,得![]() ,所以
,所以![]() .
.
![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以四边形![]() 的面积
的面积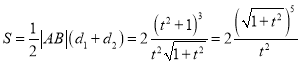 ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
所以,当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
因此,四边形![]() 的面积
的面积![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】(理)某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定:![]() 三级为合格等级,
三级为合格等级,![]() 为不合格等级.
为不合格等级.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
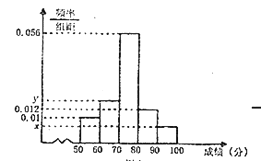
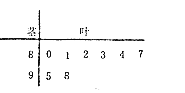
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 两个等级的学生中随机抽取了3名学生进行调研,记
两个等级的学生中随机抽取了3名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,
,![]() ,
,
(1)求![]() 在
在![]() 处的切线的一般式方程;
处的切线的一般式方程;
(2)请判断![]() 与
与![]() 的图像有几个交点?
的图像有几个交点?
(3)设![]() 为函数
为函数![]() 的极值点,
的极值点,![]() 为
为![]() 与
与![]() 的图像一个交点的横坐标,且
的图像一个交点的横坐标,且![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为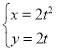 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(![]() cosθ+sinθ)=8.
cosθ+sinθ)=8.
(1)求曲线C和直线l的直角坐标方程;
(2)若射线m的极坐标方程为θ![]() (ρ≥0),设m与C相交于点M(非坐标原点),m与l相交于点N,点P(6,0),求△PMN的面积.
(ρ≥0),设m与C相交于点M(非坐标原点),m与l相交于点N,点P(6,0),求△PMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国营企业集团公司现有员工1000名,平均每人每年创造利润10万元.为了激化内部活力,增强企业竞争力,集团公司董事会决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业;调整后,他们平均每人每年创造利润
)名员工从事第三产业;调整后,他们平均每人每年创造利润![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() %.
%.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则实数![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆相交于点
的直线与椭圆相交于点![]() ,
,![]() 两点(两点均在
两点(两点均在![]() 轴的上方),且
轴的上方),且![]() ,
,![]()
(1)若![]() ,求椭圆的方程;
,求椭圆的方程;
(2)直线![]() 的斜率;
的斜率;
(3)求![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极稳妥疫情期间的复学工作,市教育局抽调5名机关工作人员去某街道3所不同的学校开展驻点服务,每个学校至少去1人,若甲、乙两人不能去同一所学校,则不同的分配方法种数为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com