(本小题满分12分)
已知等差数列 满足:
满足: ,
, .
. 的前n项和为
的前n项和为 .
.
(1)求 及
及 ;
;
(2)若 ,
, (
(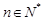 ),求数列
),求数列 的前
的前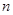 项和
项和 .
.
(1)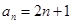 ,
,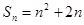 (2)
(2)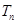 =
=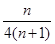
解析试题分析:(1)设等差数列{an}的首项为a1,公差为d
∵ 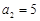 ,
,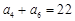 ∴
∴ 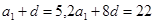
解得 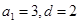 ∴
∴ 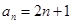
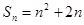 , ………………6分
, ………………6分
(2)∵ 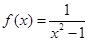 ,
,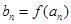 ∴
∴ 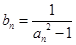 ………………7分
………………7分
∵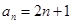 ∴
∴ 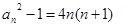
∴ 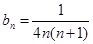
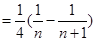

= 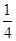 (1-
(1- 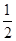 +
+ 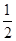 -
- 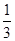 +…+
+…+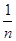 -
-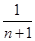 ) =
) =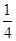 (1-
(1-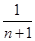 ) =
) =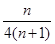
所以数列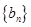 的前
的前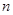 项和
项和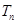 =
=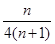 . ……12分
. ……12分
考点:等差数列求通项求和及一般数列求和
点评:本题数列 求和采用的是裂项相消的方法,此外常用到的一般数列求和有分组求和,倒序相加求和,错位相减求和,其中错位相减法求和是常考的知识点,本题属于中档题
求和采用的是裂项相消的方法,此外常用到的一般数列求和有分组求和,倒序相加求和,错位相减求和,其中错位相减法求和是常考的知识点,本题属于中档题

