【题目】学校为了了解高三学生每天自主学习中国古典文学的时间,随机抽取了高三男生和女生各50名进行问卷调查,其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”,否则为“非古文迷”,调查结果如表:
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据表中数据判断能否有![]() 的把握认为“古文迷”与性别有关?
的把握认为“古文迷”与性别有关?
(2)先从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;
(3)现从(2)中所抽取的5人中再随机抽取3人进行体育锻炼时间的调查,记这3人中“古文迷”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
参考公式: 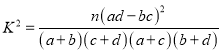 ,其中
,其中![]() .
.
参考答案:
【答案】(1)见解析;(2)5人中“古文迷”和“非古文迷”的人数分别为3人和2人;(3)见解析.
【解析】试题分析:(1)通过列联表求得![]() ,对应查表下结论;
,对应查表下结论;
(2)利用分层抽样的原理,根据比例求人数即可;
(3)利用超几何分布的原理求分布列即可.
试题解析:
(1)由列联表得![]() ,
,
所以没有![]() 的把握认为“古文迷”与性别有关.
的把握认为“古文迷”与性别有关.
(2)调查的50名女生中“古文迷”有30人,“非古文迷”有20人,按分层抽样的方法抽出5人,则“古文迷”的人数为![]() 人,“非古文迷”有
人,“非古文迷”有![]() 人.
人.
即抽取的5人中“古文迷”和“非古文迷”的人数分别为3人和2人.
(3)因为![]() 为所抽取的3人中“古文迷”的人数,所以
为所抽取的3人中“古文迷”的人数,所以![]() 的所有取值为1,2,3.
的所有取值为1,2,3.
![]() ,
, ![]() ,
, ![]() .
.
所以随机变量![]() 的分布列为
的分布列为
| 1 | 2 | 3 |
|
|
|
|
于是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量产品中某种元素的含量(单位:毫克),如图是测量数据的茎叶图:
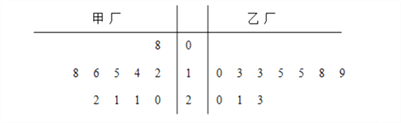
规定:当产品中的此种元素含量不小于16毫克时,该产品为优等品.
(1)从乙厂抽出的上述10件样品中,随机抽取3件,求抽到的3件样品中优等品数
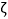 的分布列及其数学期望
的分布列及其数学期望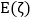 ;
;(2)从甲厂的10件样品中有放回地逐个随机抽取3件,也从乙厂的10件样品中有放回地逐个随机抽取3件,求抽到的优等品数甲厂恰比乙厂多2件的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
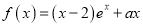 .(
.( 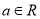 )
)(I)试确定函数
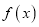 的零点个数;
的零点个数;(II)设
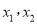 是函数
是函数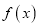 的两个零点,当
的两个零点,当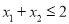 时,求
时,求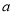 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
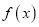 的定义域为
的定义域为 ,对于任意的
,对于任意的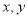 都有
都有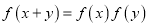 ,设
,设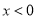 时,
时, 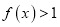 .
.(1)求
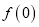 ;
;(2)证明:对于任意的
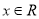 ,
, 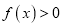 ;
;(3)当
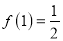 时,若不等式
时,若不等式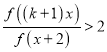 在
在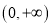 上恒定成立,求实数
上恒定成立,求实数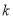 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌手机销售商今年1,2,3月份的销售量分别是1万部,1.2万部,1.3万部,为估计以后每个月的销售量,以这三个月的销售为依据,用一个函数模拟该品牌手机的销售量y(单位:万部)与月份x之间的关系,现从二次函数
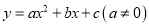 或函数
或函数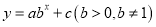 中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件.
中选用一个效果好的函数行模拟,如果4月份的销售量为1.37万件,则5月份的销售量为__________万件. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某商业公司为全面激发每一位职工工作的积极性、创造性,确保2017年超额完成销售任务,向党的十九大献礼.年初该公司制定了一个激励销售人员的奖励方案:每季度销售利润不超过15万元时,则按其销售利润的
 进行奖励;当季销售利润超过15万元时,若超过部分为
进行奖励;当季销售利润超过15万元时,若超过部分为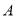 万元,则超出部分按
万元,则超出部分按 进行奖励,没超出部分仍按季销售利润的
进行奖励,没超出部分仍按季销售利润的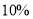 进行奖励.记奖金总额为
进行奖励.记奖金总额为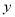 (单位:万元),季销售利润为
(单位:万元),季销售利润为 (单位:万元).
(单位:万元).(Ⅰ)请写出该公司激励销售人员的奖励方案的函数表达式;
(Ⅱ)如果业务员李明在本年的第三季度获得5.5万元的奖金,那么,他在该季度的销售利润是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
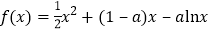 .
.(Ⅰ)讨论
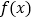 的单调性;
的单调性;(Ⅱ)设
 ,证明:当
,证明:当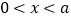 时,
时, ;
;(Ⅲ)设
 是
是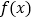 的两个零点,证明
的两个零点,证明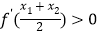 .
.
相关试题

