【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,动直线
,动直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.![]() 为坐标原点,
为坐标原点,![]() 是
是![]() 中点.
中点.
(1)若![]() ,求
,求![]() 的面积;
的面积;
(2)若试探究是否存在常数![]() ,使得
,使得![]() 是定值?若存在,求
是定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)存在;
(2)存在;![]()
【解析】
(1)利用椭圆的几何性质,求得椭圆的方程,当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,联立方程,求得
,联立方程,求得![]() 的坐标,结合面积公式,即可求解;
的坐标,结合面积公式,即可求解;
(2)设![]() ,
,![]() ,联立
,联立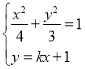 求得
求得![]() ,
,![]() ,再利用向量的数量积的运算公式,化简
,再利用向量的数量积的运算公式,化简![]() ,得到常数
,得到常数![]() 时,得出定值,得到结论.
时,得出定值,得到结论.
(1)由题意,椭圆![]() 的离心率为
的离心率为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ,
,
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
联立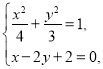 消去
消去![]() ,整理得
,整理得![]() ,解得
,解得![]() ,
,![]() ,
,
可得![]() ,
,![]() ,
,
所以![]() 的面积为
的面积为![]() .
.
(2)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
联立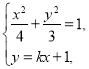 得
得![]() ,
,
其判别式![]() ,所以
,所以![]() ,
,![]() ,
,
从而![]()
![]()
![]()
![]()
![]()
![]() ,
,
所以当![]() 时,
时,![]() ,
,
即![]() 为定值,
为定值,
故存在常数![]() ,使得
,使得![]() 为定值
为定值![]() .
.

