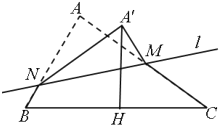
【题目】如图，在中，，，.过的中点的动直线与线段交于点.将沿直线向上翻折至，使得点在平面内的投影落在线段上.则点的轨迹长度为________.

【答案】

【解析】

建立空间坐标系，求出的轨迹，根据折叠过程中量之间的关系的，可得的取值范围，进而得到圆心角，从而弧长即点的轨迹长度.

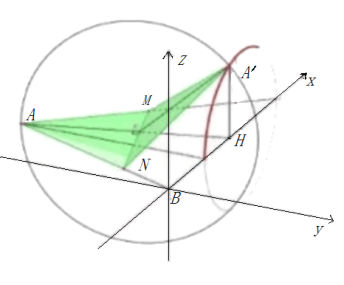
因为翻折前后长度不变，所以点可以在空间中看做以为球心，AC为直径的球面上，又因为的投影始终在上，所以点所在的面垂直于底面，

故点轨迹为垂直于底面ABC的竖直面去截球所得圆面的圆弧，这个圆弧的直径为时，的长度（由余弦定理可得，所以此时），

如图，以底面点B为空间原点建系，根据底面几何关系，

得点，点，

设点，翻折后点的投影在轴上，

所以点纵坐标为0，即由，，

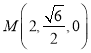根据空间两点之间距离公式可得轨迹：，

又因为动点要符合空间面翻折结论：，

即，其中，

又动点N在线段AB上动，设，

故，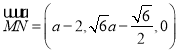

且，由，可计算得横坐标范围为，

且点在上方，由，计算可得圆弧所在扇形圆心角为，

所以弧长为.

故答案为：.

关闭